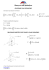Całki podwójne - Katedra Matematyki, Politechnika Białostocka

Całki podwójne
Całki podwójne po prostokacie.
˛
Całki podwójne po obszarach normalnych.
Zamiana zmiennych w całkach podwójnych.
Zastosowania całek podwójnych.
Małgorzata Wyrwas
Katedra Matematyki
Wydział Informatyki
Politechnika Białostocka
Całki podwójne – str. 1/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Podział prostokata
˛
Podziałem prostokata
˛ P nazywamy zbiór ∆n złożony z
prostokatów
˛
P1 , P2 , . . . , Pn , które całkowicie wypełniaja˛ prostokat
˛
P oraz maja˛ parami rozłaczne
˛
wn˛etrza (tzn. (intPi ) ∩ (intPj ) = ∅,
dla i 6= j).
y
d
P2 P3
Pk
∆yk
P1
c
∆xk
a
b
x
Całki podwójne – str. 2/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Oznaczenia w definicji całki po prostokacie
˛
∆xk , ∆yk - wymiary prostokata
˛ Pk , gdzie 1 ¬ k ¬ n;
dk =
q
(∆xk )2 + (∆yk )2 - długość przekatnej
˛
prostokata
˛ Pk ,
gdzie 1 ¬ k ¬ n;
δ(∆n ) = max dk - średnica podziału ∆n ;
1¬k¬n
A = {A1 (x∗1 , y1∗ ), A2 (x∗2 , y2∗ ), . . . , An (x∗n , yn∗ )} , gdzie
Ak (x∗k , yk∗ ) ∈ Pk dla 1 ¬ k ¬ n, A - zbiór punktów pośrednich
podziału ∆n .
Całki podwójne – str. 3/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Suma całkowa funkcji po prostokacie
˛
Niech funkcja f b˛edzie ograniczona na prostokacie
˛ P oraz niech
∆n b˛edzie podziałem tego prostokata,
˛ a A zbiorem punktów
pośrednich.
Suma˛ całkowa˛ funkcji f odpowiadajac
˛ a˛ podziałowi ∆n
oraz punktom pośrednim A nazywamy liczb˛e
n
X
f (x∗k , yk∗ ) · (∆xk ) · (∆yk ) .
k=1
Całki podwójne – str. 4/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Suma całkowa funkcji po prostokacie
˛
Uwaga: Suma całkowa jest przybliżeniem obj˛etości bryły
ograniczonej wykresem funkcji z = f (x, y) > 0 leżacym
˛
nad
prostokatem
˛
P oraz płaszczyzna˛ XOY przez obj˛etości
prostopadłościanów o podstawach Pk i wysokościach f (x∗k , yk∗ ),
dla 1 6 k 6 n.
Całki podwójne – str. 5/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki podwójne po prostokacie
˛
Niech funkcja f b˛edzie ograniczona na prostokacie
˛ P.
Całk˛e podwójna˛ funkcji f po prostokacie
˛ P definiujemy wzorem
x
P
def
f (x, y)dxdy =
lim
n
X
δ(∆n )→0 k=1
f (x∗k , yk∗ ) · (∆xk ) · (∆yk ) ,
o ile granica po prawej stronie znaku równości jest właściwa i nie
zależy od sposobu podziału ∆n prostokata
˛ P ani od sposobu
wyboru punktów pośrednich A. Mówimy wtedy, że funkcja f jest
całkowalna na prostokacie
˛ P.
Całki podwójne – str. 6/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki podwójne po prostokacie
˛
Całk˛e podwójna˛ z funkcji f po prostokacie
˛ P oznaczamy też
symbolem:
x
f (x, y)dP .
P
Całka podwójna po prostokacie
˛ jest uogólnieniem całki z funkcji
jednej zmiennej po przedziale.
Całki podwójne – str. 7/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Twierdzenie o całkowalności funkcji ciagłych:
˛
Funkcja ciagła
˛ na prostokacie
˛ jest na nim całkowalna.
Twierdzenie o liniowości całki:
Niech funkcje f i g b˛eda˛ całkowalne na prostokacie
˛ P oraz niech
α, β ∈ R. Wtedy
x
P
[αf (x, y) + βg(x, y)] dxdy = α
x
f (x, y)dxdy + β
P
x
g(x, y)dxdy .
P
Całki podwójne – str. 8/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Twierdzenie o addytywności całki wzgl˛edem obszaru całkowania
Jeżeli funkcja f jest całkowalna na prostokacie
˛ P , to dla
dowolnego podziału tego prostokata
˛ na prostokaty
˛ P1 i P2 o
rozłacznych
˛
wn˛etrzach zachodzi równość
x
P
f (x, y)dxdy =
x
f (x, y)dxdy +
P1
x
f (x, y)dxdy .
P2
Całki podwójne – str. 9/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Twierdzenia o zamianie całki podwójnej na całk˛e iterowana˛
Jeżeli funkcja f jest całkowalna na prostokacie
˛
P = ha, bi × hc, di, to
x
P
f (x, y)dxdy =
Zb h Zd
a
c
i
f (x, y)dy dx
=
Zd h Zb
c
i
f (x, y)dx dy .
a
Całki podwójne – str. 10/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całk˛e iterowana˛
Zb h Zd
a
i
f (x, y)dy dx
c
możemy zapisywać umownie
Zb
dx
a
Zd
f (x, y)dy .
c
Podobna˛ umow˛e możemy przyjać
˛ dla drugiej całki iterowanej, tzn.
Zd h Zb
c
a
i
f (x, y)dx dy =
Zd
c
dy
Zb
f (x, y)dx .
a
Całki podwójne – str. 11/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
π π π
Niech P = − ,
× 0,
.
4
4
4
x
Obliczyć
sin(x + y)dxdy .
P
Całki podwójne – str. 12/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całka podwójna z funkcji o rozdzielonych zmiennych
Jeżeli funkcja f jest funkcja˛ postaci f (x, y) = g(x) · h(y), gdzie g
i h sa˛ ciagłe
˛ odpowiednio na przedziałach ha, bi i hc, di, to
x
P
g(x) · h(y)dxdy =



Zb
a
 
 
g(x)dx · 
Zd
c


h(y)dy 
.
Całki podwójne – str. 13/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech P = h0, 1i × h−1, 1i.
Obliczyć
x
ex+y dxdy .
P
Całki podwójne – str. 14/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki podwójne po obszarach
Niech f b˛edzie funkcja˛ określona˛ i ograniczona˛ w obszarze
ograniczonym D ⊂ R2 oraz niech P b˛edzie dowolnym
prostokatem
˛
zawierajacym
˛
obszar P .
Ponadto niech f ∗ oznacza rozszerzenie funkcji f na P określone
wzorem:
∗
def
f (x, y) =

f (x, y),
0,
dla (x, y) ∈ D,
dla (x, y) ∈ P \ D.
Całki podwójne – str. 15/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki podwójne po obszarach
Całk˛e podwójna˛ funkcji f po obszarze D definiujemy wzorem:
x
def
f (x, y)dxdy =
x
f ∗ (x, y)dxdy ,
P
D
o ile całka po prawej stronie znaku równości istnieje.
Mówimy wtedy, że funkcja f jest
Całka
s
całkowana w obszarze D .
f ∗ (x, y)dxdy nie zależy od wyboru prostokata
˛ P.
P
Całki podwójne – str. 16/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Obszary normalne wzgl˛edem osi układu
1
Obszar domkni˛ety D nazywamy
obszarem normalnym wzgl˛edem osi OX, jeżeli można go
zapisać w postaci:
D = {(x, y) : a 6 x 6 b ∧ g(x) 6 y 6 h(x)} ,
gdzie funkcje g i h sa˛ ciagłe
˛ na ha, bi, przy czym g(x) < h(x)
dla x ∈ (a, b).
Całki podwójne – str. 17/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Obszary normalne wzgl˛edem osi układu
2
Obszar domkni˛ety D nazywamy
obszarem normalnym wzgl˛edem osi OY , jeżeli można go
zapisać w postaci:
D = {(x, y) : c 6 y 6 d ∧ p(y) 6 x 6 q(y)} ,
gdzie funkcje p i q sa˛ ciagłe
˛ na hc, di, przy czym p(y) < q(y)
dla y ∈ (c, d).
Całki podwójne – str. 18/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Obszar D ograniczony krzywymi y = 0, x = 2 i y = x jest
2
obszarem normalnym zarówno wzgl˛edem osi OX jak również
wzgl˛edem osi OY .
Obszar D ograniczony krzywymi y = −1, y = 1,
q
x = 2 − 1 − y2 i x =
q
1 − y 2 − 1 jest obszarem
normalnym wzgl˛edem osi OY .
Całki podwójne – str. 19/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki iterowane po obszarach normalnych
Jeżeli funkcja f jest ciagła
˛ na obszarze domkni˛etym
D = {(x, y) : a 6 x 6 b ∧ g(x) 6 y 6 h(x)}
normalnym wzgl˛edem osi OX, to
x
D
f (x, y)dxdy =
Zb h h(x)
Z
i
f (x, y)dy dx .
a
g(x)
Całki podwójne – str. 20/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całki iterowane po obszarach normalnych
Jeżeli funkcja f jest ciagła
˛ na obszarze domkni˛etym
D = {(x, y) : c 6 y 6 d ∧ p(y) 6 x 6 q(y)}
normalnym wzgl˛edem osi OY , to
x
D
f (x, y)dxdy =
Zd h q(y)
Z
c
p(y)
i
f (x, y)dx dy .
Całki podwójne – str. 21/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech D = {(x, y) : y > x ∧ y 6 3x − x2 }.
Obliczyć
x 2
x − xy dxdy .
D
Całki podwójne – str. 22/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Obszar regularny na płaszczyźnie
Sum˛e skończonej liczby obszarów normalnych wzgl˛edem osi
układu o parami rozłacznych
˛
wn˛etrzach nazywamy
obszarem regularnym na płaszczyźnie.
Całki podwójne – str. 23/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Całka po obszarze regularnym
Niech obszar regularny D = D1 ∪ D2 ∪ . . . ∪ Dn i
intDi ∩ intDj = ∅, dla i 6= j oraz niech funkcja f b˛edzie
całkowalna na D. Wtedy
x
D
f (x, y)dxdy =
x
f (x, y)dxdy+
D1
+
x
f (x, y)dxdy + . . . +
D2
x
f (x, y)dxdy.
Dn
Całki podwójne – str. 24/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech D = {(x, y) : xy 6 1 ∧ |x − y| 6 1}.
Obliczyć
x
xydxdy .
D
Całki podwójne – str. 25/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Wartość średnia funkcji f w obszarze D
Wartościa˛ średnia˛ funkcji f na obszarze D nazywamy liczb˛e
1 x
fśr =
f (x, y)dxdy ,
|D| D
def
gdzie |D| oznacza pole obszaru D.
Wartość średnia funkcji f w obszarze D jest równa wysokości walca o
podstawie D, który ma t˛e sama˛ obj˛etość co bryła V .
Całki podwójne – str. 26/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Wartość średnia funkcji f w obszarze D
Przykład. Wysokość nad poziomem morza pewnego terenu jest
opisana wzorem w(x, y) = 20 + sin x cos 2y, gdzie
π π
(x, y) ∈ h0, πi × − ,
. Oblicz średnie wzniesienie tego
2 2
terenu.
Twierdzenie: Jeżeli funkcja f jest ciagła
˛ na obszarze normalnym
D, to w tym obszarze istnieje punkt (x0 , y0 ), taki że
fśr = f (x0 , y0 ) .
Całki podwójne – str. 27/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przekształcenia obszarów na płaszczyźnie
Niech ∆ ⊂ R2 i D ⊂ R2 b˛eda˛ obszarami odpowiednio na
płaszczyznach U OV i XOY .
Przekształceniem obszaru ∆ w obszar D nazywamy funkcj˛e
F : ∆ → D określona˛ wzorem
(x, y) = F(u, v) = (ϕ(u, v), ψ(u, v)) ,
gdzie (u, v) ∈ ∆.
def
F (∆) = {(x, y) : x = ϕ(u, v) ∧ y = ψ(u, v) ∧ (u, v) ∈ ∆} F (∆)obraz zbioru ∆.
Jeżeli funkcje ϕ, ψ sa˛ ciagłe
˛ na obszarze ∆, to przekształcenie F nazywamy ciagłym.
˛
Jeżeli różnym punktom obszaru ∆ odpowiadaja˛ różne punkty jego obrazu D, to przekształcenie F
nazywamy różnowartościowym.
AUTOMATYKA I R OBOTYKA , SEM . II,
Całki podwójne – str. 28/46
rok. akad. 2009/2010
Przekształcenia obszarów na płaszczyźnie
JF (u, v) =
∂ϕ
(u, v)
∂u
∂ψ
(u, v)
∂u
∂ϕ
∂v (u, v)
∂ψ
∂v (u, v)
- jakobian przekształcenia F .
Twierdzenie: Obraz obszaru przy przekształceniu ciagłym
˛
i
różnowartościowym jest również obszarem.
Przykład: Niech F (u, v) = (u + v, u − v) i
∆ = {(u, v) : 0 6 u 6 1 ∧ 2 6 v 6 4}.
Całki podwójne – str. 29/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zamiana zmiennych w całkach podwójnych
Niech
przekształcenie F odwzorowuje różnowartościowo wn˛etrze
obszaru regularnego ∆ na wn˛etrze obszaru regularnego D,
funkcje ϕ, ψ maja˛ ciagłe
˛ pochodne czastkowe
˛
rz˛edu pierwszego na
pewnym zbiorze otwartym zawierajacym
˛
obszar ∆,
funkcja f b˛edzie ciagła
˛ na obszarze D,
J (u, v) 6= 0, dla (u, v) ∈ int∆.
F
Wtedy
x
D
f (x, y)dxdy =
x
f (ϕ(u, v), ψ(u, v)) · |JF (u, v)| dudv .
∆
Całki podwójne – str. 30/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech D b˛edzie obszarem ograniczonym krzywymi 2x + y = 2,
2x + y = 3, x − y = −1 i x − y = 1.
Obliczyć
x
(x + y)dxdy .
D
Całki podwójne – str. 31/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Współrz˛edne biegunowe w całkach podwójnych
Położenie punktu A(x, y) na płaszczyźnie można opisać para˛ liczb
(ϕ, ̺), gdzie:
ϕ – oznacza miara kata˛ mi˛edzy dodatnia˛ cz˛eścia˛ osi OX a
promieniem wodzacym
˛
punktu A, 0 ¬ ϕ < 2π lub
−π < ϕ 6 π,
̺ – oznacza odległość punktu A od poczatku
˛ układu
współrz˛ednych, 0 6 ̺ < ∞.
Par˛e liczb (ϕ, ̺) nazywamy
współrz˛ednymi biegunowymi punktu płaszczyzny.
Całki podwójne – str. 32/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zależność mi˛edzy współrz˛ednymi biegunowymi i kartezjańskimi

x
= ̺ cos ϕ
B:
y = ̺ sin ϕ
Przekształcenie B, które każdemu punktowi (ϕ, ̺)
przyporzadkowuje
˛
punkt (x, y) określony powyższymi wzorami,
nazywamy
przekształceniem biegunowym.
Jakobian przekształcenia biegunowego JB = ̺.
Całki podwójne – str. 33/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Twierdzenie - współrz˛edne biegunowe w całce podwójnej
Niech
obszar ∆ we współrz˛ednych biegunowych b˛edzie obszarem
regularnym
funkcja f b˛edzie ciagła
˛ na obszarze D, który jest obrazem
obszaru ∆ przy przekształceniu biegunowym, tzn. D = B(∆).
Wtedy
x
D
f (x, y)dxdy =
x
f (̺ cos ϕ, ̺ sin ϕ) · ̺ d̺dϕ .
∆
Całki podwójne – str. 34/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech D b˛edzie obszarem ograniczonym krzywa˛ x2 + y 2 = 1.
Obliczyć
x
ln(1 + x2 + y 2 )dxdy .
D
Całki podwójne – str. 35/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Przykład
Niech D b˛edzie obszarem ograniczonym krzywa˛ x2 + y 2 = 2.
Obliczyć
x
−(x2 +y 2 )
e
dxdy .
D
Całki podwójne – str. 36/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w geometrii
Pole obszaru
Pole obszaru regularnego D ⊂ R2 wyraża si˛e wzorem:
|D| =
x
dxdy .
D
Całki podwójne – str. 37/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w geometrii
Obj˛etość bryły
Obj˛etość bryły V położonej nad obszarem regularnym D ⊂ R2 i
ograniczonej z dołu i z góry odpowiednio wykresami funkcji
ciagłych
˛
z = d(x, y) i z = g(x, y) wyraża si˛e wzorem:
|V | =
x
[g(x, y) − d(x, y)] dxdy .
D
Całki podwójne – str. 38/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w geometrii
Pole płata
Pole płata Σ, który jest wykresem funkcji z = f (x, y), gdzie
(x, y) ∈ D wyraża si˛e wzorem:
|Σ| =
v
x u
u
t
D
∂f
1+
∂x
!2
∂f
+
∂y
!2
dxdy .
Całki podwójne – str. 39/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w mechanice
Masa obszaru
Masa obszaru D ⊂ R2 o g˛estości powierzchniowej masy ρ wyraża
si˛e wzorem:
M=
x
ρ(x, y)dxdy .
D
Całki podwójne – str. 40/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w mechanice
Momenty statyczne
Momenty statyczne wzgl˛edem osi OX i OY obszaru D ⊂ R2 o
g˛estości powierzchniowej masy ρ wyrażaja˛ si˛e wzorami:
M Sx =
x
yρ(x, y)dxdy ,
D
M Sy =
x
xρ(x, y)dxdy .
D
Całki podwójne – str. 41/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Zastosowania całek podwójnych w mechanice
Współrz˛edne środka masy
Współrz˛edne środka masy obszaru D ⊂ R2 o g˛estości
powierzchniowej masy ρ wyrażaja˛ si˛e wzorami:
M Sy
xC =
,
M
M Sx
.
yC =
M
Całki podwójne – str. 42/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Momenty bezwładności
Momenty bezwładności wzgl˛edem osi OX, OY obszaru D ⊂ R2
o g˛estości powierzchniowej masy ρ wyrażaja˛ si˛e wzorami:
Ix =
x
y 2 ̺(x, y)dxdy ,
D
Iy =
x
x2 ̺(x, y)dxdy .
D
Całki podwójne – str. 43/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Moment bezwładności wzgl˛edem punktu O(0, 0)
Moment bezwładności wzgl˛edem punktu O(0, 0) obszaru D ⊂ R2
o g˛estości powierzchniowej masy ρ wyraża si˛e wzorem:
IO =
x
(x2 + y 2 )̺(x, y)dxdy .
D
Całki podwójne – str. 44/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Podsumowanie
Całki podwójne po prostokacie.
˛
Całki podwójne po obszarach normalnych.
Zamiana zmiennych w całkach podwójnych.
Współrz˛edne biegunowe w całkach podwójnych.
Zastosowania całek podwójnych.
Całki podwójne – str. 45/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010
Dzi˛ekuj˛e za uwag˛e ;)
Całki podwójne – str. 46/46
AUTOMATYKA I R OBOTYKA , SEM . II,
rok. akad. 2009/2010