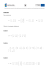1 Wydział: WILiŚ, Transport, sem.2 dr Jolanta Dymkowska Przykład

1
Wydział: WILiŚ, Transport, sem.2
dr Jolanta Dymkowska
Przykład: Zbadać wzajemne położenie dwóch prostych. Jeżeli proste przecinają się, znaleźć
punkt przeciącia prostych oraz kat między prostymi:
l1 :




x = 1



l2 :
y = −2 + 3 t





 z = t


 3x − y − 2z = 0
x + y − 2z = 0


Rozwiązanie:
• Prosta l2 dana jest równaniem w pstaci krawędziowej. Zapiszemy ją więc w postaci
parametrycznej. W tym celu rozwiążemy układ równań:


 3x − y − 2z = 0


x + y − 2z = 0
Rząd macierzy głównej tego układu, jak i rząd macierzy rozszerzonej jest równy 2 ,
ponadto
3
1
−1 6= 0.
1 Weźmy więc z = t . Wówczas x = t i y = t . Stąd równanie parametryczne prostej l2
ma postać:
l2 :




x = t



y = t





 z = t
• Dla prostej l1 jej wektor kierunkowy ma współrzedne ~a1 = [0, 3, 1] a punkt P1 (1, −2, 0)
należy do tej prostej. Analogicznie dla prostej l2 : ~a2 = [1, 1, 1] i P2 (0, 0, 0).
• Liczymy iloczyn mieszany:
( ~a1 × ~a2 ) ◦ P1~P2
0
= 1
−1
3
1
2
1 1 = 2 − 3 + 1 = 0.
0 2
Ponieważ ( ~a1 × ~a2 ) ◦ P1~P2 = 0 , to proste l1 i l2 są współpłaszczyznowe.
• Obliczmy kąt pomiedzy tymi prostymi:
cos α =
| ~a1 ◦ ~a2 |
4
4
= √ √ = √ .
| ~a1 | · | ~a2 |
10 3
30
• Obliczamy punkt przecięcia prostych, rozwiązując układ równań:




1



−2 + 3 t





 t
= s
= s
= s
Jest to układ trzech równań z dwoma niewiadomymi. Z geometrii wiemy, że układ ten ma
dokładnie jedno rozwiązanie: t = s = 1 . Stąd punkt przecięcia prostych ma współrzędne
P (1, 1, 1) .