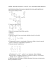∑ b ∑ ∑

 a1

a
A =  2
 ...

 a k






a1b1 a1b2 ... a1bw 


a b a b ... a2bw 
A* B' =  2 1 2 1
 ...
... ... ... 


akb1 akb1 ... akbw 
 b1

b
B =  2
 . ..

 b w






 t i ,1

t i ,2
Ti = 
 ...

 t i , k






 v i ,1

v i ,2
Vi = 
 ...

 v i , k






 a1 + b1 


a2 + b2 

A+ B =
 ... 


 ak + bk 
 a1 + c 


a + c
A+c =  2
 ... 


 ak + c 
A ' =  T1
 a1 ⋅ c 


a ⋅ c
A⋅c =  2
 ... 


 a k ⋅ c 
'
B = b1 b2 ... bw 
A' + c =  a1 + c
A' ⋅ c =  a1 ⋅ c
a 2 + b2
...
a k + bk 
 t1,1 
 
 t1,2
A'⋅ B =  
...
 
t1,k 

a 2 + c ... a k + c 
a 2 ⋅ c ... a k ⋅ c 
A ⋅B =
∑
k
i =1
a i ⋅b i
 t 2,1 


 t 2,2 
 ... 


 t 2,k 
...
 t w ,1  


 t w ,2  
 ...  


 t w ,k  
v1,k  


v 2 ,2 ... v 2 ,k  

...

v w ,2 ... v w ,k  

v1,2
...
 v v ... v  
1,k 
 t2,1 
 tw,1    1,1 1,2

 
  



t
t
...
v
v
v
2,k  
 2,2  ...  w,2  ⋅   2,1 2,2
 ... 
 ...  

...
 
  

tw,k  v
t2,k 

...
v
v
w
,1
w
,2
w
,
k


∑ ∑
k
'
k
Ti ⋅Vi '
ai ⋅bi =
i =1
A' ⋅ B =
...

 V1'    v1,1
 ' 
v
V 
B =  2  =   2 ,1

 ...  
V '  
v
 w 
  w ,1
A' = a1 a2 ... ak 
A ' + B ' =  a1 + b1
T2
  t1,1 
 
 t1,2
Tk  =   
 ... 
 
  t1,k 

i =1
Przykład
Ti
 t i ,1

=  t i ,2
t
 i ,3
V
 v i ,1 
= 

 v i , 2 
i





 t 
 1,1 
T2  = t1,2 
 t 
 1,3 
'
A = T1
 V '    v1,1
B =  1'  = 
V 2    v 2 ,1
 
∑
 t2,1 
 
t2,2 
 
t2,3 
v1,2  


v 2 ,2  

k
'
A ⋅B =
∑
k
a i ⋅bi =
i =1
 t1,1 
 
T1 ⋅ V1 =  t1,2  ⋅  v1,1
t 
 1,3 
'
T2 ⋅ V 2
T1 ⋅ V1'
'
'
i =1
 t1,1 ⋅ v1,1

v1,2  =  t1,2 ⋅ v1,1
t ⋅v
 1,3 1,1
 t 2 ,1 


=  t 2 ,2  ⋅  v 2 ,1
t 
 2 ,3 
 t1,1 ⋅ v1,1

+ T2 ⋅ V2 =  t1,2 ⋅ v1,1
t ⋅ v
 1,3 1,1
'
∑
k
A ⋅B =
i =1
Ti ⋅V i ' = T1 ⋅ V1' + T2 ⋅ V 2 '
t 
  1,1 
ai ⋅bi =   t1,2 
 t 
 1,3 
t1,1 ⋅ v1,2 

t1,2 ⋅ v1,2 
t1,3 ⋅ v1,2 
 t 2 ,1 ⋅ v 2 ,1

v 2 ,2  =  t 2 ,2 ⋅ v 2 ,1
t ⋅v
 2 ,3 2 ,1
t1,1 ⋅ v1,2   t2,1 ⋅ v2,1
 
t1,2 ⋅ v1,2  +  t2,2 ⋅ v2,1
t1,3 ⋅ v1,2   t2,3 ⋅ v2,1
 t2,1   
     v1,1
 t2,2   ⋅ 
 t    v2,1
 2,3 
t 2 ,1 ⋅ v 2 ,2 

t 2 ,2 ⋅ v 2 ,2 
t 2 ,3 ⋅ v 2 ,2 
t2,1 ⋅ v2,2   t1,1 ⋅ v1,1 + t2,1 ⋅ v2,1
 
t2,2 ⋅ v2,2  =  t1,2 ⋅ v1,1 + t2,2 ⋅ v2,1
t2,3 ⋅ v2,2   t1,3 ⋅ v1,1 + t2,3 ⋅ v2,1

v1,2    t1,1 ⋅ v1,1 + t2,1 ⋅ v2,1
 = t ⋅v + t ⋅v
 1,2 1,1 2,2 2,1
 
v2,2 
  t1,3 ⋅ v1,1 + t2,3 ⋅ v2,1
t1,1 ⋅ v1,2 + t2,1 ⋅ v2,2 

t1,2 ⋅ v1,2 + t2,2 ⋅ v2,2 
t1,3 ⋅ v1,2 + t2,3 ⋅ v2,2 
t1,1 ⋅ v1,2 + t2,1 ⋅ v2,2 

t1,2 ⋅ v1,2 + t2,2 ⋅ v2,2 
t1,3 ⋅ v1,2 + t2,3 ⋅ v2,2 
Rząd macierzy
Jeżeli dla liniowej kombinacji n wektorów Ci równej 0:
∑
n
ci Ai = 0
i=1
(1) ISTNIEJE niezerowy wektor C, to wektory Ci są ZALEŻNE liniowo
(2) Tylko zerowy wektor C zapewnia równość, to wektory Ci są NIEzależne liniowo
Rząd macierzy A [w x k] to maksymalna liczba jej niezależnych liniowo wektorów.
r(A) ≤ min (w,k); r(A) = wymiar maksymalnej podmacierzy o niezerowym wyznaczniku,
którą można wyodrębnić z A.
O macierzach kwadratowych:
Dopełnienie algebraiczne wyrazu ai,j macierzy A oznaczane A i,j jest to iloczyn (-1)(i+j) oraz
wyznacznika podmacierzy macierzy A uzyskanej przez usunięcie z macierzy A i-tego wiersza
i j-tej kolumny
Macierz dołączona do A oznacza się adj (A)
Jest to transponowana macierz dopełnień algebraicznych wszystkich jej wyrazów.
T
b 
A 
B=adj(A) Ù  j , k  =  k , j 
gdzie Ai,j jest dopełnieniem algebraicznym wyrazu i,j macierzy A
bk,j jest wyrazem macierzy B i równa się Aj,k
Odwrotność macierzy A oznacza się A-1
B=A-1 Ù BA=I=AB
Macierz odwrotną względem macierzy A uzyskujemy pod warunkiem, że macierz A ma
niezerowy wyznacznik z macierzy dołączonej dzieląc jej wyrazy przez wyznacznik macierzy
A:
A-1 = adj(A)/|A|
Zatem wyrazem bk,j macierzy B=A-1 jest iloraz A j,k / |A|
Uzasadnienie:
Wyraz (i,j) macierzy A A-1 =
∑
n
ai ,k ⋅ bk , j =
k =1
∑
n
ai ,k ⋅
k =1
Aj ,k
A
∑
n
= A⋅
ai ,k ⋅ Aj ,k
k =1
suma ta jest równa 0, gdy i≠j. Gdy i=j suma jest wyznacznikiem macierzy A, zaś wyraz (i,j)
macierzy A A-1 jest równy 1.
Rozwiązywanie układu równań liniowych.
Liniowa zależność wektorów.
Wektory A1,A2,A3, ...An, wszystkie o tej samej liczbie wyrazów, są zależne liniowo, jeżeli
istnieje n liczb x1, x2, x3, ..., xn, z których co najmniej jedna jest różna od 0 takich, że suma
iloczynów
∑
n
x i Ai = 0
i =1
jest wektorem zerowym.
Jeżeli wektory nie są zależne liniowo, to są niezależne liniowo.
(1) Jeżeli wśród wektorów jest wektor zerowy, to te wektory są zależne liniowo.
(2) Każdy podzbiór zbioru wektorów niezależnych liniowo jest zbiorem wektorów
niezależnych liniowo
(3) Jeżeli liczba wyrazów w wektorze jest mniejsza od liczby wektorów, to te wektory są
liniowo zależne
Rząd macierzy.
Rzędem macierzy A mającej m wierszy i n kolumn oznaczanym r(A) jest liczebność
największego podzbioru jej kolumn lub wierszy będącego podzbiorem wektorów
niezależnych liniowo.
(1) r(A) ≤ min(m,w)
(2) r(A) = wymiar (stopień) największej kwadratowej podmacierzy wyodrębnionej z A,
która ma niezerowy wyznacznik.
Układ m jednorodnych równań liniowych z n niewiadomymi x1,x2,...,xn:
a11x1 + a12x2 + a13x3 + … + a1nxn = 0
a21x1 + a22x2 + a23x3 + … + a2nxn = 0
………………………………………
am1x1 + am2x2 + am3x3 + … + amnxn = 0
można zapisać w postaci macierzowej:
Ax = 0
gdzie:
 a1,1 a1,2

a2,1 a2,2
A= 
 ... ...

am,1 am,2
 x1 
 
x
x =  2  ;0 =
 ... 
 
 xn 
... a1,n 

... a2,n 
... ... 

... am,n 
0
 
0
...
 
 0 
„Ax = 0” można zapisać inaczej:
a1,1

a2,1
A⋅ x = 
...

am,1
a1,2
a2,2
...
am,2
...
...
...
...
 a1,1x1 + a1,2x2 +

a2,1x1 + a2,2x2 +
= 
... +
... +

am,1x1 + am,2x2 +
a1,n  x1
 
a2,n  x2
⋅
=
...  ... 
 
amn,  xn
... + a1,nxn   a1,1x1 + a1,2x2 +... + a1,nxn   a1,1x1   a1,2x2 
 a1,nxn 
 
 
 



... + a2,nxn   a2,1x1 + a2,2x2 +... + a2,nxn  a2,1x1  a2,2x2 
a2,nxn 

=
 =  ...  +  ...  +... +  ...  =
... + ...  
...
 
 
 



... + amn, xn  am,1x1 + am,2x2 +... + amn, xn  am,1x1 am,2x2 
amn, xn 
 a1,1 
 a1,2 
 a1,n 
0
 
 
 
 
a2,1 
a2,2 
a2,n 
0



=
⋅ +
⋅ + +
⋅ = 
 ...  x1  ...  x2 ...  ...  xn ...
 
 
 
 
0
am,1
am,2 
amn, 
Wektor x nazywamy wektorem pierwiastków tego układu równań lub „rozwiązaniem”.
(1) Wektor zerowy jest (trywialnym) rozwiązaniem układu równań.
(2) Warunkiem istnienia (koniecznym i wystarczającym) nietrywialnego (niezerowego)
rozwiązania układu m równań liniowych z n niewiadomymi jest to, iżby kolumny macierzy A
były zależne liniowo, bo wtedy wśród liczb x1, x2, ..., xn będzie co najmniej jedna różna od 0.
Jest to równoważne z tym, że r(A) < n.
(3) Jeżeli jakiś wektor x jest (nietrywialnym) rozwiązaniem układu równań, to iloczyn cx (c to
dowolna stała różna od 0) jest również nietrywialnym rozwiązaniem tego układu równań.
(4) Wszystkie rozwiązania układu równań liniowych są wielokrotnościami jednego
rozwiązania wtedy i tylko wtedy, gdy r(A) = n-1. ( W tej sytuacji liczba równań m musi być
większa lub równa n-1)
(5) Jeżeli r(A)=n (w tej sytuacji liczba równań m musi być większa lub równa n), to jedynym
rozwiązaniem układu równań jest wektor zerowy.