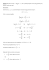Główka pracuje - zadania wymagające myślenia... czyli

Główka pracuje - zadania wymagające myślenia...
czyli TOP TRENDY nowej matury.
W tej poradzie 20 trudniejszych zadań. Wiele z nich to zadania, których temat zaczyna się od
wykaż, udowodnij…, czyli niezbyt lubianych przez maturzystów.
___________________________________________________________________________
Zadanie 1.
Wiadomo, że dla każdego x należącego do dziedziny funkcji y = f ( x ) zachodzi warunek:
1 + f ( x ) + f 2 ( x ) + ... = x 2 − 1 , gdzie lewa strona jest sumą zbieżnego szeregu geometrycznego.
Wyznacz wzór tej funkcji i jej dziedzinę.
___________________________________________________________________________
Iloraz ciągu geometrycznego wynosi q = f ( x) . Aby szereg był zbieżny, musi być spełniony
warunek: q < 1 ⇔ f ( x ) < 1
Korzystając ze wzoru na sumę szeregu geometrycznego otrzymujemy:
1
= x2 − 1
1 − f ( x)
1
1 − f ( x) = 2
x −1
1
x2 − 1 − 1 x2 − 2
f ( x) = 1 − 2
=
= 2
x −1
x2 − 1
x −1
x2 − 2
Otrzymaliśmy równanie funkcji: f ( x ) = 2
.
x −1
x2 − 2
Aby wyznaczyć dziedzinę tej funkcji, należy rozwiązać nierówność 2
< 1 , której
x −1
dziedziną jest zbiór R \ {1,−1} .
 x2 − 2
/ ⋅ ( x − 1)2
 x 2 − 1 < 1
 2
 x − 2 > −1
/ ⋅ ( x − 1)2
 x 2 − 1
 ( x 2 − 2)( x 2 − 1) < ( x 2 − 1)2
 2
2
2
2
( x − 2)( x − 1) > −( x − 1)
( x 2 − 2)( x 2 − 1) − ( x 2 − 1)2
 2
2
2
2
( x − 2)( x − 1) + ( x − 1)
( x 2 − 1) ( x 2 − 2) − ( x 2 − 1)
 2
2
2
( x − 1) ( x − 2) + ( x − 1)
 ( x 2 − 1)( −1) < 0
 2
2
( x − 1)( 2x − 3) > 0
[
[
<0
>0
]< 0
]> 0
 x2 − 1 > 0

( x − 1)( x + 1)( 2x − 3 )( 2x + 3 ) > 0
a) x 2 − 1 > 0 ⇔ x ∈ ( −∞ ,−1) ∪ (1, ∞ )
b) ( x − 1)( x + 1)( 2x − 3 )( 2x + 3 ) > 0
x1 = 1 , x 2 = − 1 , x 3 =
3
3
, x4 = −
2
2

 3 
3 


(
)
x ∈  − ∞ ,−
∪
−
1
,
1
∪

 2 ,∞
2




Otrzymaliśmy:
 x ∈ ( −∞ ,−1) ∪ (1, ∞ )

 x ∈  − ∞ ,− 3  ∪ (− 1,1) ∪  3 , ∞ 

 2 

2 





3   3 
∪
,∞ .
co daje x ∈  − ∞ ,−
2   2 

Otrzymany zbiór jest dziedziną funkcji f ( x) .
___________________________________________________________________________
Zadanie 2.
Wykaż, że jeśli równanie x 2 + px + q = 0 ma rozwiązanie, to wartość bezwzględna różnicy
jego pierwiastków jest równa pierwiastkowi wyróżnika tego równania.
___________________________________________________________________________
Równanie ma rozwiązania, czyli ∆ = p 2 − 4q ≥ 0 .
Należy udowodnić, że x1 − x 2 = ∆ , czyli ( x1 − x 2 )2 = ∆
( x1 − x 2 )2 = x12 − 2x1x 2 + x 22 = x12 + x 22 + 2x1x 2 − 4x1x 2 = ( x1 + x 2 )2 − 4x1x 2 =
korzystamy ze wzorów Viete’a
= ( −p )2 − 4q = p 2 − 4q = ∆ , co należało udowodnić.
___________________________________________________________________________
Zadanie 3.
Bok kwadratu ABCD ma długość a. Wierzchołek A połączono ze środkami E i F
odpowiednio boków BC i CD. Wykaż, że odcinki AE i AF dzielą przekątną BD na trzy
odcinki o równej długości.
___________________________________________________________________________
BD = a 2
1
1
Wystarczy udowodnić jedno z dwojga: x = a 2 lub y = a 2 .
3
3
a
1
sin α 1
W ∆ABE : tgα = 2 = , skąd mamy:
=
i sin 2 α + cos 2 α = 1
a 2
cos α 2
cos α = 2 sin α , sin 2 α + ( 2 sin α )2 = 1
5 sin 2 α = 1
1
2
, cos α =
5
5
W ∆ABP stosujemy twierdzenie sinusów:
x
a
=
0
sin α sin 180 − (450 + α )
x
a
=
1
sin 450 + α
5
a
5x =
0
sin 45 cos α + cos 450 sin α
a
a
a
2 5a
5x =
=
=
=
2 2
2 1
2
2
3 2
3 2
+
+
2 5
2 5
5 2 5 2 5
2a
2 2a 1
x=
=
= a 2 , co należało udowodnić.
3⋅ 2
3
3 2
___________________________________________________________________________
Zadanie 4.
Wykaż, że jeżeli równanie postaci x 3 + ax + b = 0 ma pierwiastek podwójny, to
4a 3 + 27b 2 = 0
___________________________________________________________________________
Jeżeli to równanie ma pierwiastek podwójny, to musi się dać zapisać w postaci:
( x − p )2 ( x − q ) = 0 , gdzie p jest pierwiastkiem podwójnym, q – drugim pierwiastkiem i
p ≠ q.
Przekształcamy to równanie:
( x 2 − 2px + p 2 )( x − q ) = 0
sin α =
(
(
)
)
x 3 − qx 2 − 2px 2 + 2pqx + p 2 x − p 2q = 0
x 3 − ( 2p + q )x 2 + ( 2pq + p 2 )x − p 2q = 0
Porównując otrzymane równanie z równaniem wyjściowym otrzymujemy:
 − 2p − q = 0

2
 2pq + p = a
 − p 2q = b

q = −2p - wstawiamy otrzymaną wartość do pozostałych dwóch równań.
 2p ⋅ ( −2p ) + p 2 = a
, co daje

2
 − p ⋅ ( −2p ) = b
a
 2
p
−
=

3

b
3
p = −
2

Z otrzymanych równań wynika, że p 6 = −
a3
b2
i p6 =
.
27
4
a3 b2
Stąd −
=
⇔ − 4a 3 = 27b 2 ⇔ 4a 3 + 27b 2 = 0 , co należało udowodnić.
27 4
___________________________________________________________________________
Zadanie 5.
a
1
Czy prawdziwe jest zdanie: V Λ x 2 + 4x +   > 0 ?
 2
a∈R x∈R
___________________________________________________________________________
a
1
Ma istnieć takie a ∈ R , by trójmian kwadratowy x + 4x +   przyjmował wartości
 2
dodatnie dla wszystkich liczb rzeczywistych x.
Taka sytuacja ma miejsce wtedy, gdy wykresem trójmianu jest parabola leżąca nad osią OX,
czyli gdy ∆ < 0 .
a
a

1
 1  

∆ = 16 − 4 ⋅   = 4 4 −  

 2
 2  

2
a
1
∆ < 0 ⇔ 4−  < 0
 2
1
 
 2
−2
1
< 
 2
a
x
1
co daje − 2 > a , bo funkcja y =   jest malejąca.
 2
Odp. Takich wartości istnieje nieskończenie wiele: a < −2 . Zdanie jest prawdziwe.
___________________________________________________________________________
Zadanie 6.
Wszystkie liczby naturalne ustawione w porządku rosnącym podzielono na grupy:
(1) , ( 2,3) , (4,5,6) , (7,8,9,10) , ...
Obliczyć sumę liczb występujących w n-tej grupie.
___________________________________________________________________________
Ilość liczb w n-tej grupie wynosi n.
Obliczymy, od jakiej liczby rozpoczyna się n-ta grupa.
W grupach: 1,2,3,…,n-1 występuje 1+2+3+…+(n-1) liczb.
1+2+3+…+(n-1) jest sumą (n-1) wyrazów ciągu arytmetycznego, dlatego
1+ n −1
n(n − 1)
1 + 2 + 3 + ... + (n − 1) =
⋅ (n − 1) =
2
2
n(n − 1)
Wobec tego n-ta grupa rozpoczyna się od liczby
+ 1 , natomiast ostatnia liczba tej
2
n(n − 1)
grupy to
+n.
2
Liczby n-tej grupy tworzą n-wyrazowy ciąg arytmetyczny, którego suma wynosi:
n(n − 1)
n(n − 1)
+1+
+n
n(n − 1) + 1 + n
n2 + 1
n3 + n
2
2
⋅n =
⋅n =
⋅n =
Sn =
, co jest
2
2
2
2
rozwiązaniem zadania.
___________________________________________________________________________
Zadanie 7.
Iloczyn skalarny wektorów AB o AC jest równy polu równoległoboku o bokach AB i AC.
Wyznaczyć miarę kąta BAC.
___________________________________________________________________________
Zgodnie z definicją iloczynu skalarnego i danymi w zadaniu:
P = AB o AC = AB ⋅ AC ⋅ cos α , gdzie P oznacza pole równoległoboku.
Z drugiej strony pole równoległoboku wynosi:
1
P = 2 ⋅ P∆ABC = 2 ⋅ ⋅ AB ⋅ AC ⋅ sin α = AB ⋅ AC ⋅ sin α
2
Mamy więc: AB ⋅ AC ⋅ cos α = AB ⋅ AC ⋅ sin α , czyli sin α = cos α , z czego wyciągamy
wniosek, że kąt BAC ma miarę α = 450 .
___________________________________________________________________________
Zadanie 8.
1 1 1
1
Wykazać, że jeżeli + + =
, to co najmniej dwie spośród liczb a,b,c są liczbami
a b c a+b+c
przeciwnymi.
___________________________________________________________________________
1 1 1
1
Wiadomo, że + + −
=0
a b c a+b+c
bc + ac + ab
1
−
=0
abc
a+b+c
(bc + ac + ab )(a + b + c) − abc
=0
abc(a + b + c)
Wobec tego musi być: (bc + ac + ab )(a + b + c) − abc = 0
(a + b )(bc + ac + ab ) + bc 2 + ac 2 + abc − abc = 0
(a + b )(bc + ac + ab ) + c 2 (a + b ) = 0
(a + b )(bc + ac + ab + c 2 ) = 0
(a + b )[b(a + c) + c(a + c)] = 0
(a + b )(a + c)(b + c) = 0
a + b = 0 ∨ a + c = 0 ∨ b + c = 0 , czyli a = −b ∨ a = −c ∨ b = −c , co należało
udowodnić.
___________________________________________________________________________
Zadanie 9.
Wykazać, że jeżeli a 2 + b 2 + c 2 = ab + ac + bc , to a = b = c .
___________________________________________________________________________
Dane: a 2 + b 2 + c 2 − ab − ac − bc = 0
/⋅ 2
2a 2 + 2b 2 + 2c 2 − 2ab − 2ac − 2bc = 0
a 2 − 2ab + b 2 + a 2 − 2ac + c 2 + b 2 − 2bc + c 2 = 0
( a − b ) 2 + (a − c ) 2 + ( b − c ) 2 = 0
Ostatnie równanie jest spełnione tylko wtedy, gdy a = b i a = c i b = c , co należało
udowodnić.
___________________________________________________________________________
Zadanie 10.
1
Wykazać, że jeżeli a + b = 1 , to a 4 + b 4 ≥ dla dowolnych liczb a i b.
8
___________________________________________________________________________
[
]
2
[
]
2
a 4 + b 4 = a 2 + b 2 − 2a 2b 2 = (a + b )2 − 2ab − 2(ab )2 =
korzystamy z założenia a + b = 1
2
= [1 − 2ab ] − 2(ab )2 = 1 − 4ab + 4(ab )2 − 2(ab )2 = 2(ab )2 − 4(ab ) + 1
Oszacujmy wyrażenie ab . Korzystając z faktu, że a + b = 1 otrzymujemy:
ab = a(1 − a ) = − a 2 + a
Funkcja f (a ) = −a 2 + a przyjmuje wartości z przedziału (− ∞ , q , gdzie q jest drugą
współrzędną wierzchołka paraboli:
−∆
12 − 4 ⋅ ( −1) ⋅ 0 1
q=
=
=
4 ⋅ ( −1)
4
4

1
Wiemy więc, że ab ∈  − ∞ , .
4


1
Przyjmijmy teraz, że t = ab , t ∈  − ∞ , .
4

Mamy a 4 + b 4 = 2t 2 − 4t + 1 = g(t )
4
= 1 , co oznacza, że funkcja
2⋅ 2

1
1
g(t) jest w przedziale  − ∞ ,
malejąca i wartość najmniejszą przyjmuje dla t = .
4
4

Pierwsza współrzędna wierzchołka tej paraboli jest równa
2
1
1
1
1
g  = 2 ⋅   − 4 ⋅ + 1 = .
4
8
 4
 4
1
, co należało udowodnić.
8
___________________________________________________________________________
Zadanie 11.
Zbadaj liczbę pierwiastków równania x 3 − (m − 2)x + 2 = 0 w zależności od parametru m.
___________________________________________________________________________
x 3 − mx + 2x + 2 = 0
mx = x 3 + 2x + 2
x 3 + 2x + 2
m=
x
x ≠ 0 - takie założenie możemy przyjąć, bo x = 0 nie jest rozwiązaniem równania
wyjściowego.
x 3 + 2x + 2
Zbadamy przebieg zmienności funkcji f ( x ) =
, x≠0
x
Stąd wniosek, że g(t ) = 2t 2 − 4t + 1 = a4 + b 4 ≥
x 3 + 2x + 2
2

= lim  x 2 + 2 +  = ∞
→
−∞
x → −∞
x → −∞
x
x
x

3
x + 2x + 2
lim− f ( x ) = lim−
= −∞ , bo licznik dąży do 2, a mianownik do 0 po wartościach
x→0
x→0
x
ujemnych
x 3 + 2x + 2
lim+ f ( x ) = lim+
= ∞ , bo licznik dąży do 2, a mianownik do 0 po wartościach
x→0
x→ 0
x
dodatnich
x 3 + 2x + 2
2

= lim  x 2 + 2 +  = ∞
lim f ( x ) = lim
→
∞
x→∞
x → −∞
x
x
x

2
3
3
( 3x + 2)x − ( x + 2x + 2) 2x − 2 2( x 3 − 1)
f ' ( x) =
=
=
x2
x2
x2
Znak pochodnej zależy od znaku wyrażenia y = x 3 − 1 , czyli dla x > 1 pochodna przyjmuje
wartości dodatnie, a dla x ∈ ( −∞ ,0) ∪ (0,1) - wartości ujemne.
−∞ ,0) i (0,1) , oraz rosnąca w
Wobec tego funkcja f ( x) jest malejąca w przedziałach (−∞
przedziale (1, ∞ ) .
Dla x = 1 funkcja osiąga minimum, które wynosi
13 + 2 ⋅ 1 + 2
f (1) =
=5
1
Przybliżony wykres funkcji f ( x) :
lim f ( x ) = lim
Z wykresu funkcji f ( x) odczytujemy, że równanie
x 3 + 2x + 2
= m ma:
x
a) jedno rozwiązanie dla m < 5
b) dwa rozwiązania dla m = 5
c) trzy rozwiązania dla m > 5
___________________________________________________________________________
Zadanie 12.

1 
1 
1
1 

Oblicz granicę lim  1 −  1 −  1 −  ⋅ ... ⋅  1 − 2  
n→∞
4 
9 
16 
n 


___________________________________________________________________________
1 3
=
4 4
1 
1 4

Dla n = 3 mamy:  1 −  1 −  =
4 
9 6

1 
1 
1 5

Dla n = 4 mamy:  1 −  1 −  1 −  =
4 
9 
16  8

1 
1 
1 
1  6

Dla n = 5 mamy:  1 −  1 −  1 −  1 −  =
4 
9 
16 
25  10

Stawiamy hipotezę, że dla n ∈ {2,3,4,...} zachodzi:
1 
1 
1
1  n+1


 1 −  1 −  1 −  ⋅ ... ⋅  1 − 2  =
4 
9 
16 
n 
2n


Udowodnimy to indukcyjnie.
Dla n = 2 już to sprawdziliśmy.
Zakładamy, że wzór ten jest prawdziwy dla pewnego n ∈ { 2,3,4,...} , tzn., że
1 
1 
1
1  n+1


.
 1 −  1 −  1 −  ⋅ ... ⋅  1 − 2  =
4 
9 
16 
n 
2n


Należy udowodnić, że twierdzenie jest prawdziwe dla liczby n + 1 , tzn.
1 
1 
1
1 
1 
n+2


=
 1 −  1 −  1 −  ⋅ ... ⋅  1 − 2  1 −
2 
4 
9 
16 
n 
(n + 1)  2(n + 1)


Liczymy:
1 
1 
1
1 
1 


 = (na mocy założenia)
 1 −  1 −  1 −  ⋅ ... ⋅  1 − 2  1 −
4 
9 
16 
n 
(n + 1)2 


Dla n = 2 mamy: 1 −
n + 1
1  n + 1 (n + 1)2 − 1 n(n + 2)
n+2
 1 −
=
, co należało udowodnić.
=
⋅
=
2 
2
2n 
(n + 1) 
2n
(n + 1)
2n(n + 1) 2(n + 1)
Liczymy granicę:
1
1+

1 
1 
1
1 
n+1

n =1
lim  1 −  1 −  1 −  ⋅ ... ⋅  1 − 2   = lim
= lim
n→∞
n→∞
4 
9 
16 
n   n → ∞ 2n
2
2


___________________________________________________________________________
Zadanie 13.
Oblicz sumę: 20052 − 20042 + 20032 − 20022 + ... + 32 − 22 + 12
___________________________________________________________________________
20052 − 20042 + 20032 − 20022 + ... + 32 − 22 + 12 =
= ( 20052 − 20042 ) + ( 2003 2 − 20022 ) + ... + ( 3 2 − 2 2 ) + 1 =
( 2005 − 2004)( 2005 + 2004) + ( 2003 − 2002)( 2003 + 2002) + ... + ( 3 − 2)( 3 + 2) + 1 =
= 4009 + 4005 + 4001 + ... + 5 + 1
Otrzymana suma jest sumą n wyrazów ciągu arytmetycznego, w którym:
a1 = 4009 , r = −4 , an = 1
an = a1 + (n − 1)r - za pomocą tego wzoru wyliczymy, ile wyrazów ciągu jest sumowanych.
1 = 4009 + (n − 1)( −4)
0 = 4008 − 4n + 4
4n = 4012
n = 1003
=
Szukana suma wynosi:
a + an
Sn = 1
n=
(n=1003)
2
4009 + 1
=
⋅ 1003 = 2005 ⋅ 1003 = 2011015
2
___________________________________________________________________________
Zadanie 14.
Udowodnij, że liczba a jest wielokrotnym pierwiastkiem wielomianu W(x) wtedy i tylko
wtedy, gdy jest wspólnym miejscem zerowym wielomianu W(x) i jego pochodnej.
___________________________________________________________________________
A.
Zakładamy, że liczba a jest wielokrotnym pierwiastkiem wielomianu W(x), tzn.
W( x ) = ( x − a )n ⋅ Q( x ) , n ∈ { 2,3,4,...}
Należy udowodnić, ze liczba a jest także pierwiastkiem W' ( x) .
W' ( x ) = n ⋅ ( x − a )n − 1 ⋅ Q( x ) + ( x − a )n Q' ( x ) = ( x − a )n − 1 [nQ( x ) + ( x − a )Q' ( x )]
Z otrzymanego równania wynika, że W' (a) = 0 , czyli liczba a jest pierwiastkiem W' ( x) .
B
Załóżmy teraz odwrotnie, ze liczba a jest wspólnym pierwiastkiem W( x) i W' ( x) , czyli
W(a) = 0 i W' (a) = 0 .
Należy udowodnić, że liczba a jest pierwiastkiem wielokrotnym wielomianu W(x).
W(a) = 0 , czyli W( x ) = ( x − a)P( x) , gdzie P(x) jest pewnym wielomianem.
W' ( x) = P( x) + ( x − a )P' ( x)
Wiemy, że W' (a) = 0 , czyli P(a) + (a − a)P' (a) = 0 .
Stąd P(a) = 0 , czyli a jest pierwiastkiem wielomianu P(x). Wielomian P(x) można więc
zapisać w postaci P( x) = ( x − a)M( x) .
W( x ) = ( x − a )P( x ) = ( x − a )( x − a )M( x ) = ( x − a )2 M( x )
Stąd wniosek, że liczba a jest co najmniej dwukrotnym pierwiastkiem wielomianu W(x), co
kończy dowód.
___________________________________________________________________________
Zadanie 15.
Pary (x,y) liczb całkowitych, spełniające równanie x 3 − x 2 y + xy − y 2 = 5 są współrzędnymi
wierzchołków pewnego wielokąta wypukłego. Oblicz pole tego wielokąta.
___________________________________________________________________________
x 3 − x 2 y + xy − y 2 = 5
x2 (x − y ) + y(x − y ) = 5
( x − y )( x 2 + y ) = 5
Skoro x i y są liczbami całkowitymi, to musi być:
x−y =5
 x − y = −5
 x−y =1
 x − y = −1
lub  2
lub  2
lub  2
 2
x + y = 1
 x + y = −1
x + y = 5
 x + y = −5
 y = x−5
 y = x+5
 y = x−1
 y = x+1
lub  2
lub  2
lub  2
 2
x + x − 6 = 0
x + x + 6 = 0
x + x − 6 = 0
x + x + 6 = 0
Drugi i czwarty układ nie mają rozwiązań.
Rozwiązaniem równania x 2 + x − 6 = 0 jest x = −3 ∨ x = 2 .
 x = −3
 x = −3
⇔ 

y = x − 5
 y = −8
 x=2
x=2
⇔ 

y = x − 5
 y = −3
 x = −3
 x = −3
⇔ 

y = x − 1
 y = −4
 x=2
x = 2
⇔ 

y = x − 1
y = 1
Otrzymaliśmy punkty: A = ( −3,−8) , B = ( 2,−3) , C = ( 2,1) , D = ( −3,−4)
Czworokąt ABCD jest równoległobokiem (wykonanie rysunku zostawiamy czytelnikowi), o
podstawie AD = 4 i wysokości 5.
Jego pole: P = 4 ⋅ 5 = 20 j2
___________________________________________________________________________
Zadanie 16.
Iloczyn trzech liczb pierwszych równa się ich pięciokrotnej sumie. Jakie to liczby?
___________________________________________________________________________
Oznaczmy szukane liczby: x,y,z.
Szukamy ich w zbiorze {2,3,4,...} , gdyż są liczbami pierwszymi.
xyz = 5( x + y + z )
Prawa strona równania dzieli się przez 5, więc lewa również dzieli się przez 5.
Stąd wniosek, że jedna z tych liczb (x albo y albo z) musi być równa 5.
Przyjmijmy, że z = 5 . Wtedy:
5xy = 5( x + y + 5)
xy = x + y + 5
xy − y = x + 5
y( x − 1) = x + 5
x+ 5 x−1+ 6 x −1
6
6
=
=
y=
+
= 1+
x−1
x−1
x−1 x−1
x−1
y jest liczbą całkowitą, więc 6 musi dzielić się przez x − 1 i x ∈ { 2,3,4,...} .
Wobec tego x − 1 ∈ {1,2,3,6} , czyli x ∈ { 2,3,4,7} .
Spośród tych czterech liczb, liczbami pierwszymi są x1 = 2 , x 2 = 3 , x 4 = 7 .
Liczymy odpowiadające im wartości y:
2+5
3+5
7+5
y1 =
=7
y2 =
=4
y3 =
=2
2−1
3−1
7−1
y 2 odrzucamy, bo 4 nie jest liczbą pierwszą.
z = 5
z = 5


Otrzymaliśmy:  x = 2 lub  x = 7
y = 7
y = 2


Szukane liczby pierwsze to 2, 5, 7.
___________________________________________________________________________
Zadanie 17.
Wyznacz wszystkie pary (x,y) liczb całkowitych spełniające układ równań
 x+y =6
 x
y
 2 + 3 = 25
___________________________________________________________________________
Liczby 2 x i 3y są dodatnie, wobec tego:
2x < 25 , czyli x < 5 , oraz 3y < 25 , czyli y < 3 .
Z pierwszego równania: y = 6 − x , co daje 6 − x < 3 ⇔ x > 3 .
x < 5 , x > 3 i x jest liczbą całkowitą, więc x = 4 .
y = 6−x= 6−4= 2
Odp. istnieje tylko jedna taka para: x = 4 i y = 2 .
___________________________________________________________________________
Zadanie 18.
Liczby a1 , a 2 , a 3 ,..., an są kolejnymi wyrazami ciągu geometrycznego. Znając sumy:
1
1
1
1
+
+ ... +
S = a1 + a 2 + a 3 + ... + an oraz T = +
a1 a 2 a 3
an
oblicz iloczyn I = a1 ⋅ a 2 ⋅ a 3 ⋅ ... ⋅ an
___________________________________________________________________________
Przyjmijmy: a1 = a, a 2 = aq, a 3 = aq 2 ,..., an = aq n − 1
S
S = a + aq + aq 2 + ... + aq n − 1 = a(1 + q + q 2 + ... + q n − 1 ) , stąd: 1 + q + q 2 + ... + q n − 1 =
a
S
1 1
1
1
q n − 1 + q n − 2 + q n − 3 + ... + q + 1
S
T= +
+ 2 + ... + n − 1 =
= an − 1 = 2 n − 1
n −1
a aq aq
aq
aq
aq
aq
S
Daje to: a 2qn − 1 =
T
Obliczymy teraz szukany iloczyn:
I = a ⋅ aq ⋅ aq 2 ⋅ ... ⋅ aq n − 1 = an ⋅ q ⋅ q 2 ⋅ q 3 ⋅ ... ⋅ q n − 1 = an ⋅ q1+ 2 + 3 + ... + ( n − 1) =
korzystamy ze wzoru na sumę wyrazów ciągu arytmetycznego
=a q
n
1+ n −1
( n − 1)
2
=a q
n
n( n −1)
2
n
 n 2− 1 
= aq  = a 2q n − 1


(
)
1
n
2
=
korzystamy z obliczonej wcześniej wartości a 2qn − 1 =
S
T
n
 S 2
= 
T
n
 S 2
Odp. Szukany iloczyn wynosi  
T
___________________________________________________________________________
Zadanie 19.
Wiedząc, że log 98 56 = p obliczyć log 7 14 .
___________________________________________________________________________
98 = 2 ⋅ 7 2 oraz 56 = 7 ⋅ 23 .
log b x
Skorzystamy ze wzoru na zmianę podstawy logarytmu log a x =
:
log b a
log 2 56 log 2 (7 ⋅ 2 3 ) log 2 7 + log 2 2 3
log 2 7 + 3
=
=
=
2
2
log 2 98 log 2 ( 2 ⋅ 7 ) log 2 2 + log 2 7
1 + 2 log 2 7
log 2 7 + 3
Z równania
= p obliczymy log 2 7 :
1 + 2 log 2 7
3 + log 2 7 = p + 2p log 2 7
2p log 2 7 − log 2 7 = 3 − p
( 2p − 1) log 2 7 = 3 − p
3−p
log 2 7 =
2p − 1
Podobnie zmieniamy podstawę logarytmu dla szukanego log 7 14 .
log 2 14 log 2 ( 2 ⋅ 7) log 2 2 + log 2 7 1 + log 2 7
log 7 14 =
=
=
=
=
log 2 7
log 2 7
log 2 7
log 2 7
i wstawiamy obliczony wcześniej log 2 7
3−p
1+
2p − 1 2p − 1 + 3 − p 2p − 1 p + 2
=
=
⋅
=
, co należało obliczyć.
3−p
2p − 1
3−p 3−p
2p − 1
___________________________________________________________________________
Zadanie 20.
Wyznaczyć resztę z dzielenia wielomianu W( x ) = x100 − 2x 99 + 2x 50 − 1 przez wielomian
p = log 98 56 =
G( x) = x 3 − x
___________________________________________________________________________
Wielomian W(x) dzielimy przez wielomian stopnia trzeciego, więc reszta z dzielenia ma
postać ax 2 + bx + c .
G ( x ) = x 3 − x = x( x 2 − 1) = x( x − 1)( x + 1)
Wielomian W(x) można przedstawić w postaci:
W( x ) = G ( x ) ⋅ P( x ) + ax 2 + bx + c , gdzie P(x) jest wynikiem z dzielenia.
x100 − 2x 99 + 2x 50 − 1 = x( x − 1)( x + 1)P( x ) + ax 2 + bx + c
Wstawiając do ostatniego równania kolejno liczby x1 = 0 , x 2 = 1 , x 3 = −1 otrzymujemy układ
równań:

 c = −1
−1= c
 c = −1



1 − 2 + 2 − 1 = a + b + c ⇔ a + b − 1 = 0 ⇔  a = 3
1 + 2 + 2 − 1 = a − b + c
a − b − 1 = 4
b = − 2



2
Szukana reszta ma postać 3x − 2x − 1 .
___________________________________________________________________________