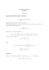∫ f (x)dx=∫

8. Całkowanie numeryczne
Wprowadzenie (8.1)
Całkowaniem numerycznym nazywamy obliczanie całki oznaczonej funkcji
dyskretnej.
Tabela wartości funkcji dyskretnej y = f(x)
Obliczanie numerczne całki jednokrotnej nosi nazwę kwadratury, a całki
wielokrotnej kubatury. Odpowiednie wzory całkowania numerycznego
nazywamy wzorami kwadratur (kubatur).
Kwadratura (kubatura) polega na zastąpieniu w przedziale całkowania [a ; b]
funkcji podcałkowej y = f(x) funkcją aproksymującą lub interpolującą y = F(x) i
przyjęciu równości
b
b
∫ f ( x) dx=∫ F ( x )dx+R f ,
a
a
gdzie RF oznacza błąd metody całkowania.
(8.1)
8. Całkowanie numeryczne
Wprowadzenie [cd.] (8.1)
- Całkowanie numeryczne umożliwia obliczanie całki oznaczonej funkcji
empirycznej - tabela przedstawia wówczas zapisane wyniki określonego
doświadczenia.
- Całkowanie numeryczne umożliwia obliczanie całki oznaczonej funkcji,
której funkcja pierwotna nie daje się przedstawić w postaci sperpozycji
skończonej liczby funkcji elementarnych (np.: f ( x)=e−x , g ( x)=sin x 2 ).
Aby obliczyć całkę oznaczoną takiej funkcji, należy najpierw utworzyć tablicę
wartości tej funkcji, a następnie zastosować metodę całkowania numerycznego.
2
Jeśli w charakterze funkcji y = f(x) przyjmiemy wielomian interpolacyjny, to wzór
(8.1) przyjmie postać
b
n
∫ f ( x) dx=∑ A j f ( x j ) dx+R f ,
a
j=0
w którym xj są wybranymi węzłami interpolacji, Aj stałymi współczynnikami
zależnymi od sposobu wyboru węzłów i niezależnymi od postaci funkcji
y = f(x), a RF błedem metody całkowania.
8. Całkowanie numeryczne
Wprowadzenie [cd.] (8.1)
Kwadratury Newtona-Cotesa (8.2)
Wzory całkowania numerycznego, w których przyjęto, że wszystkie węzły
interpolacji są rozmieszczone w jednakowych odstępach, noszą nazwę
wzorów Newtona-Cotesa. Praktycznie nie stosuje się wzorów Newtona-Coresa
opartych na wielomianach interpolacyjnych wysokich stopni.
Złożony wzór trapezów (8.2.1)
Przedział całkowania [a ; b] dzielimy na n podprzedziałów równej długości,
h n=
b−a
,
n
przy czym: x0 = a, xj = x0 + jhn dla j = 1, 2, …, n
(xn = b).
W każdym podprzedziale [ xj ; xj+1 ] ( j = 0, 1, …, n-1 ) funkcję podcałkową
y = f(x) zastępujemy wielomianem pierwszego stopnia (wielomiany są na ogół
różne w różnych podprzedziałach). Wzór (8.2) przyjmuje postać
b
∫ f ( x) dx=h n
a
(
2
(b−a) h n ' '
1
1
y0 + y1 + y 2+...+ y n−1 + y n −
f ( cn ) ,
2
2
12
przy czym a < cn < b.
)
(8.3)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór trapezów [cd.] (8.2.1)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór trapezów [cd.] (8.2.1)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór trapezów [cd.] (8.2.1)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór trapezów [cd.] (8.2.1)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór parabol (wzór Simpsona) (8.2.2)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór parabol (wzór Simpsona) [cd.] (8.2.2)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór parabol (wzór Simpsona) [cd.] (8.2.2)
Kwadratury Newtona-Cotesa (8.2)
Złożony wzór parabol (wzór Simpsona) [cd.] (8.2.2)
√
5
(b−a) M 4
n⩾
180 ε
4