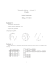Imię Nazwisko . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . grupa .... rz. .... kol

Imię Nazwisko . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
grupa .... rz. .... kol....
Produktem grafów G i H (oznaczenie G×H) nazywamy graf taki, że V (G×H) = V (G)×V (H)
oraz E(G × H) = {(u1 , u2 )(v1 , v2 ) : u1 = v1 i u2 v2 ∈ E(H) lub u1 v1 ∈ E(G) i u2 = v2 }.
1. Graf K5 × K3 ma cykl Hamiltona
2. Graf K5 × K3 ma obwód Eulera
3. χ0 (K5 × K3 ) =
4. κ(K5 × K3 ) =
5. Jeśli G jest ma obwód Eulera i co najmniej 3 wierzchołki to κ0 (G) ≥ 2.
6. Udowodnić, że jeśli G jest grafem regularnym, dwudzielnym o co najmniej 3 wierzchołkach
to κ(G) ≥ 2.
7. Udowodnić, że χ0 (G2 ) ≤ (χ0 (G))2 + 1, gdzie G2 jest grafem powstałym z G przez dodanie
krawędzi łączących wierzchołki o wspólnym sąsiedzie w G.
8. Każdy graf 4-regularny zawiera 2-regularny podgraf rozpinający. Wsk 4 jest liczbą parzystą,
a każda składowa spójności jest spójna.
Imię Nazwisko . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
grupa .... rz. .... kol....
Produktem grafów G i H (oznaczenie G×H) nazywamy graf taki, że V (G×H) = V (G)×V (H)
oraz E(G × H) = {(u1 , u2 )(v1 , v2 ) : u1 = v1 i u2 v2 ∈ E(H) lub u1 v1 ∈ E(G) i u2 = v2 }.
1. Graf K4 × K4 ma cykl Hamiltona
2. Graf K4 × K4 ma obwód Eulera
3. χ0 (K4 × K4 ) =
4. κ0 (K4 × K4 ) =
5. Jeśli G jest ma cykl Hamiltona co najmniej 3 wierzchołki to κ(G) ≥ 2.
6. Udowodnić, że jeśli δ(G) ≥ n+k−2
to κ(G) ≥ k.
2
0
0
7. Udowodnić, że χ (L(G)) ≤ 2(χ (G)) − 1, gdzie L(G) = (E(G), F ), gdzie F = {e1 e2 : e1 , e2 ∈
E(G), e1 ∩ e2 6= ∅}.
8. Udowodnić, że krawędzie dowolnego grafu można skierować w taki sposób, że w każdym
wierzchołków różnica między liczbą wchodzących i wychodzących będzie co najwyżej jeden.
Wsk. każdy graf jest albo nie jest eulerowski.