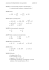PROCESY STOCHASTYCZNE

PROCESY STOCHASTYCZNE - Lista zerowa
Wydział Matematyki, kier. matematyka, studia magisterskie, I rok.
W poniższych zadaniach (Wt )t≥0 jest procesem Wienera.
Zad.1 Przypomnij postulaty procesu Wienera i wyprowadź z nich wzór na jego funkcję kowariancji.
Zad.2 Sprawdź, czy procesy
1
Xt = √ Wt√5 ,
5
są także procesami Wienera.
Zt = −Wt ,
Yt = 1(0,∞) (t)tW1/t
Zad.3 Dla jakich wartości stałych a > 0 i b, c ∈ R proces
a
Bt = b(1 + 2t)W 1+2t
− cWa ,
t≥0
jest procesem Wienera?
Zad.4 Niech (Ft ) będzie filtracją generowaną przez proces Wienera (Wt )t≥0 . Sprawdź, czy procesy
1
Wt , Wt2 − t, exp(αWt − α2 t) (α ∈ R)
2
są martyngałami względem (Ft ).
Zad.5 Uzasadnij, że dla dowolnych a, b > 0 zachodzi
P(−at < Wt < bt dla dostatecznie dużych t) = 1.
Zad.6 Oblicz
P(W2 ≤
√
2(W3 − W2 ) ≤
√
3W2 ,
W2 ≥ 0)
oraz
P(2W32 + 3W22 − 4W2 W3 ≤ 4).
Zad.7 Niech W = (W1 , . . . , Wn ) będzie procesem Wienera w Rn . Dla ustalonego t > 0 wyznacz
gęstość zmiennej losowej
Xt = W12 (t) + . . . + Wn2 (t)
przy założeniu, że W (0) = 0.
Zad.8 Niech (Wt )t≥0 będzie procesem Wienera. Udowodnij, że dla α > 3/2 całka
Z ∞
Ws
ds
sα
2
jest bezwzględnie zbieżna z prawdopodobieństwem 1.
Zad.9 Niech (Wt )t≥0 będzie procesem Wienera. Uzasadnij, że dla µ > 0
lim arctan(Wt − µt) = −π/2,
t→∞
z prawd. 1.
Co można powiedzieć o powyższej granicy w przypadku µ < 0 oraz µ = 0?
Zad.10 Korzystając z zasady odbicia uzasadnij, że gęstość procesu maksimum
Mt = max Ws
s∈[0,t]
zadana jest wzorem
r
ft (x) =
Wyznacz EMt oraz VarMt .
2
2
x
exp −
1[0,∞) (x).
πt
2t