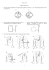Repetytorium VI

Zadania 6
Dynamika bryły sztywnej. Zasada zachowania momentu pędu.
1. W wierzchołkach kwadratu o boku a znajdują się masy punktowe m. Wyznacz moment bezwładności
tego układu względem osi obrotu która przechodzi przez: a) jeden z boków kwadratu; b) symetralną boku
kwadratu; c) przekątną kwadratu.
2. Jednorodny walec o masie M i promieniu r umocowano tak, że może on się obracać bez tarcia względem
własnej osi, która jest pozioma i nieruchoma. Na walec nawinięto nieważką nić, na końcu której zawieszono
ciało o masie m. Wyznacz przyspieszenie, z jakim będzie opadać ciało o masie m, wiedząc, że nić nie ślizga
się po walcu.
3. Kulę o masie m i promieniu r położono na szczycie równi pochyłej o długości l i kącie nachylenia α.
Korzystając z: a) zasad dynamiki; b) zasady zachowania energii, wyznaczyć prędkość środka masy u podstawy
równi, przy założeniu, że kula stacza się z równi bez poślizgu.
4. Jednorodna kula o masie m i momencie bezwładności I toczy się bez poślizgu po poziomej powierzchni z
prędkością v. Oblicz: a) moment pędu kuli względem jej środka; b) energię kinetyczną kuli.
5. Student trzymający w rozpostartych rękach ciężarki, obraca się względem pionowej osi siedząc na krzesełku
obrotowym z okresem 2 s. Przyjmijmy, że student siedzi na krzesełku obrotowym w ten sposób, że oś obrotu
stanowi jednocześnie jego oś symetrii. Jaką pracę musi wykonać student, aby przyciągnąć ciężarki z odległości
0, 7 m na odległość 0, 1 m do osi obrotu? Student trzyma w każdej ręce ciężarek o masie 3 kg. Załóżmy, że
moment bezwładności studenta względem osi obrotu jest stały i wynosi 0, 6 kgm2 .
Praca domowa
1. Jednorodny walec umocowano tak, że może on się obracać bez tarcia względem własnej osi, która jest
pozioma i nieruchoma. Na walec nawinięta jest nieważka i nierozciągliwa nić. Walec ma promień r, a jego
masa wynosi m. Jaką siłą trzeba ciągnąć nić, aby w ciągu czasu t1 walec osiągnął prędkość kątową ω1 ? 1
2. Cienkościenną rurę i jednorodny walec położono na szczycie równi pochyłej o długości l i kącie nachylenia
α. Porównać prędkości środka masy tych ciał u podstawy równi oraz przyspieszenia liniowe środka masy,
przy założeniu, że oba ciała staczają się z równi bez poślizgu i że mają one ten sam promień r oraz masę m.
2
3. Dziewczynka o masie m1 stoi na brzegu nieruchomej karuzeli o promieniu R i momencie bezwładności
I, która może obracać się bez tarcia. W pewnej chwili dziewczynka rzuca poziomo kamień o masie m2 z
prędkością v w kierunku stycznym do zewnętrznej krawędzi karuzeli. Jaka jest prędkość liniowa dziewczynki
po wyrzuceniu kamienia? 3
1
2
3
ODP 1: F = mrω√
1 /2t1 .
ODP 2: vr /vw = 3/2, ar /aw = 3/4.
ODP 3: vd = m2 vR2 /(I + m1 R2 ) .