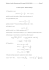Lista zada« nr 13: funkcje dwóch zmiennych

Lista zada« nr 13: funkcje dwóch zmiennych
(1) Sprawd¹, czy istniej¡ granice:
lim arctg
y
x→0
y→0
x
,
lim x arctg
x→0
y→0
xy 2
lim
,
x→0 x2 + y 2
y→0
y x
,
lim y arctg
jest jednorodn¡ funkcj¡ wektora
Sprawd¹ ponadto, »e je±li
f
~v ,
y x→0
y→0
xy 2
lim
,
x→0 x4 + y 2
y→0
x
,
x3 y 4
lim
.
x→0 x4 + y 16
y→0
(2) Sprawd¹, »e pochodna kierunkowa funkcji
~v
tzn.
f w ustalonym punkcie
0
0
fk~
v (x0 , y0 ) = kf~v (x0 , y0 )
w kierunku
dla
k > 0.
jest ró»niczkowalna, to pochodna kierunkowa jest
wr¦cz funkcj¡ liniow¡ wektora
~v .
(3) Rozwa»my funkcj¦

3
 xy
f (x, y) = x2 + y 6

0
Wyznacz pochodn¡ kierunkow¡
gdy
(x, y) 6= (0, 0),
gdy
(x, y) = (0, 0).
f w (0, 0) w kierunku wektora ~v = (vx , vy ).
(0, 0)? Czy funkcja ta jest ci¡gªa w (0, 0)?
Czy
funkcja ta jest ró»niczkowalna w
(4) Rozwa»my funkcj¦

xy
p
x2 + y 2
f (x, y) =

0
Czy funkcja ta jest
(x, y) 6= (0, 0),
gdy
(x, y) = (0, 0).
(0, 0) w kierunku wektora ~v = (cos(α), sin(α)).
ró»niczkowalna w (0, 0)? Czy funkcja ta jest ci¡gªa w (0, 0)?
Wyznacz pochodn¡ kierunkow¡
f
gdy
w
(5) Trzej przyjaciele wyje»d»aj¡ z Wrocªawia.
Pierwszy, jad¡c w kierunku ‘rody
‘l¡skiej (DK94, kierunek: zachód) z pr¦dko±ci¡
peratura ro±nie z szybko±ci¡
3 deg /h.
90 km/h,
zaobserwowaª, »e tem-
Drugi jedzie w kierunku Warszawy (S8, kie-
runek: póªnocny wschód) z pr¦dko±ci¡
120 km/h
i zaobserwowaª to samo tempo
wzrostu temperatury. Trzeci jedzie do Opola (A4, kierunek: poªudniowy wschód)
140 km/h.
z pr¦dko±ci¡
jaciel?
Jak szybkie zmiany temperatury obserwuje trzeci przy-
W którym kierunku nale»y si¦ uda¢, by temperatura rosªa najszybciej?
Poczy«my tu wszystkie niezb¦dne niezyczne zaªo»enia (Wrocªaw jest punktem,
drogi s¡ proste, temperatura jest ró»niczkowalna).
(6) Wyznacz pochodne cz¡stkowe funkcji:
arctg
y
x
,
p
ln( x2 + y 2 ),
ln
x−y
x+y
(7) Znajd¹ przykªad ró»niczkowalnej funkcji dwóch zmiennych
(x1 , y1 )
oraz
(x2 , y2 )
,
f
x
xy .
oraz dwóch punktów
o nast¦puj¡cej wªasno±ci: nie istnieje punkt po±redni
(x, y)
taki, »e
q
|f (x2 , y2 ) − f (x1 , y1 )|
p
= (fx0 (x, y))2 + (fy0 (x, y))2
(x2 − x1 )2 + (y2 − y1 )2
(co byªoby naiwnym dwuwymiarowym odpowiednikiem twierdzenia Lagrange'a o
warto±ci ±redniej).