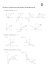O błą dze niu nie zu peł nie przy pad ko wym

fizyka wczoraj, dziś i jutro
O błądzeniu niezupełnie
przypadkowym
n HIERONIM LALEK, BARTOSZ LALEK
Fizyka w szkole, którą zajmują się nauczyciele, to głównie działalność dydaktyczna
w kształcie ustalonym przez treści wynikające
z podstawy programowej, przydziałów godzin,
stanu bazy pomocy naukowych, wybranych
programów, przyjętych podręczników itd.
Te i wiele innych czynników tworzą „klimat nauczania” decydujący o jego wynikach i poczucie sensu pracy nauczyciela.
Twórczym aspektem naszej działalności
jest rozwiązywanie problemów, które pojawiają się na lekcjach spontanicznie, a także
przy okazji olimpiad, referatów, na stronach podręczników i czasopism lub w toku
głębszych rozważań i dyskusji.
Zdarza się, że dostrzeżone problemy
wyglądają na pierwszy rzut oka banalnie,
a jednak ich rozwiązanie okazuje się dość
skomplikowane.
Chcemy przedstawić przykład takiego
problemu, którego rozwiązanie kosztowało
nas sporo wysiłku, a prześledzenie i zrozumienie całego toku rozwiązania wymaga
trochę czasu i koncentracji, a dla autentycznie zainteresowanego czytelnika jest
nawet poświęceniem.
Dla nas praca nad jego rozwiązaniem,
stanowiła odskocznię od szkolnej rzeczywistości i niełatwą próbę sił.
A oto treść problemu: w tomie I, części 2
Feynmana Wykładów z fizyki, w temacie
„Błądzenie przypadkowe”, autor przypomina problem pijanego marynarza, w ten
oto sposób: „Marynarz wychodzi z baru
i robi kilka kroków, ale każdy krok jest
skierowany pod innym kątem, na chybił
trafił. Pytamy: gdzie znajdzie się marynarz
po upływie dłuższego czasu? Oczywiście,
nie wiadomo! Nie możemy na to odpowie-
14
dzieć. Co najwyżej wiemy tylko, że znalazł
się w jakimś miejscu przypadkowo”.
Postanowiliśmy rozwiązać trochę inny
i specyficzny problem marynarza, który po
wyjściu z baru będąc pod wpływem alkoholu, chce trafić do domu (celu).
Marynarz ten ma jednak świadomość, że
jego stan umożliwia mu stawianie kroków
o takiej samej długości, naprzemian w prawo i w lewo, zawsze prostopadle do prostej
łączącej jego aktualne położenie z punktem wyjścia, po każdym wykonanym kroku.
Dylematem marynarza jest prawidłowe
wykonanie pierwszego kroku, którego
orientacja zadecyduje czy marynarz trafi
do celu, poruszając się w płaskim terenie.
Wprowadzamy kilka umownych oznaczeń i pojęć niezbędnych dla dalszych rozważań zaznaczonych na rysunku 1.
O – punkt wyjścia marynarza (bar);
P – punkt docelowy (dom);
punkty O i P wyznaczają kierunek celu
(prosta, na której leżą);
αn – kąt położenia po n-tym kroku – kąt
pomiędzy kierunkiem celu, a kierunkiem odcinka łączącego punkt wyjścia O z położeniem 1, 2, 3, ..., n, po
wykonaniu n-tego kroku;
βn – kąt odchylenia – kąt zawarty pomiędzy dwoma odcinkami łączącymi
punkt wyjścia z dwoma kolejnymi
położeniami.
Zakładamy, że kąt położenia po pierwszym kroku jest mniejszy od 45° bo inaczej
kontakt z kierunkiem celu tracony jest natychmiastowo.
Analizując geometryczne zależności wynikające z przyjętych założeń możemy zapisać:
fizyka w szkole
fizyka wczoraj, dziś i jutro
Znak „+” przy α1 występuje dla n-nieparzystej liczby kroków, „–” dla n-parzystej
liczby kroków.
Po postawieniu kolejnych kroków odległość marynarza od punktu wyjścia – zaniedbując jednostki – wynosi:
1, 2 , 3 , ..., n .
Zaś sinusy kątów odchylenia tworzą
ciąg:
1
1
, sin β3 =
,
2
3
1
1
.
sin β 4 =
, ..., sin β n =
4
n
sin β 2 =
Wstawiając do wzoru (1) zależności wynikające z powyższych ustaleń otrzymamy:
αn = arc sin β n − arc sin β n −1 +
+ arc sin β n − 2 − arc sin β n −3 + ... ± α1 =
1
1
− arc sin
+
n
n −1
1
1
+ arc sin
− arc sin
... ± α1.
n−2
n−3
= arc sin
Prawdopodobieństwo osiągnięcia celu
przez marynarza będzie maksymalne, gdy
w miarę rosnącej ilości przebytych kroków
kąt celu będzie malał i zmierzał do zera.
Skupiamy się nad obliczeniem takiego
kata α1 (orientacji pierwszego kroku),
przy którym kąt położenia zmierza do zera
dla dużej ilości wykonywanych kroków.
Wyrażenie na α zapisujemy w dwóch równaniach:
Rys. 1.
n ⎛
1
1 ⎞
α2 n +1 = ∑ ⎜ arcsin
− arcsin
⎟ + α1 ,
2n + 1
2n ⎠
n =1 ⎝
α1 = β1
α2 = β2 – α1
α3 = β3 – α2 = β3 – β2 + α1
α4 = β4 – α3 = β4 – β3 + β2 – α1
α5 = β5 – α4
.............
= β5 – β4 + β3 – β2 + α1
Uogólniając: otrzymany wzór na wartość n-tego kąta położenia:
αn = βn – βn–1 + βn–2 – βn–3 + ... + ±α1 (1)
2/2009
otrzymując kąty o numerach nieparzystych:
α3, α5, α7, ... oraz
n ⎛
1
1 ⎞
α2 n = ∑ ⎜ arc sin
− arc sin
⎟+
2n
2n − 1 ⎠
n=2 ⎝
+ arc sin
1
− α1 ,
2
otrzymując kąty o numerach parzystych:
α4, α6, α8, ...
Przy ustalonym kącie α1, kąt α2 = 45° – α1.
15
fizyka wczoraj, dziś i jutro
Sytuacja staje się realna nieprzypadkowo, gdy szeregi, którymi są powyższe
wyrażenia są zbieżne przy n zmierzającej do nieskończoności.
Przyjmując oznaczenia:
∞
⎡
n =1
⎢⎣
∞
⎡
n=2
⎢⎣
∑ ⎢arc sin
∑ ⎢arc sin
+ arc sin
1
1 ⎤
− arc sin
⎥ = Λ1 ,
2n + 1
2n ⎥⎦
1
− arc sin
2n
1 ⎤
⎥+
2n − 1 ⎥⎦
1
= Λ2,
2
można udowodnić, że:
Λ1 = –Λ2 oraz Λ1 < 0 i Λ2 > 0
Co sprawia, że z równań:
Λ1 + α1 = 0
Λ2 – α1 = 0
Rys. 2.
Tabela 1.
n
16
k = 2n
Λn1
k = 2n + 1
Λn2
10
20
0,56069
21
0,34070
11
22
0,55555
23
0,34550
100
200
0,48471
201
0,41411
101
202
0,48453
203
0,41429
200
400
0,47436
401
0,42440
201
402
0,47430
403
0,42446
500
1000
0,46516
1001
0,43356
501
1002
0,46515
1003
0,43358
1000
2000
0,46055
2001
0,43819
1001
2002
0,46054
2003
0,43819
5000
10000
0,45437
10001
0,44436
5001
10002
0,45437
10003
0,44437
10000
20000
0,45290
20001
0,44583
10001
20002
0,45290
20003
0,44583
Otrzymamy taką samą wartość kąta
pierwszego kierunku α1, gdy obliczymy
wartość Λ1 lub Λ2.
Oznaczamy bezwzględne wartości |Λ1| = |Λ2| = Λ.
Zatem poszukiwany kąt
(Λn1 + Λn2):2
pierwszego kroku α1 = Λ
0,45069
Wykorzystując standardowy
pro
gram komputerowy obli0,45052
czyliśmy wartości bezwzględ0,44941
ne częściowych sum dla wybranych i rosnących n, którym
0,44941
odpowiada parzysta liczba kro0,44938
ków k = 2n i nieparzysta liczba
kroków k = 2n + 1, umieszcza0,44938
jąc wyniki w tabeli 1.
0,44937
Oznaczyliśmy:
– sumy odpowiadające paΛ
n1
0,44937
rzystej liczbie kroków – le0,49937
wa strona kierunku celu,
Λn2 – sumy odpowiadające nie0,49937
parzystej liczbie kroków
0,49937
– prawa strona kierunku
ce
lu.
0,49937
Wartości n zostały tak wy0,44936
brane, by otrzymane wyniki dawa
ły informacje o zachowaniu
0,44936
się częściowych sum, odpowia-
fizyka w szkole
fizyka wczoraj, dziś i jutro
dających rosnącym wartościom liczby kroków i zarazem numerom położenia k, odpowiednio po lewej i prawej stronie kierunku celu, a także jak zachowują się sumy dla
wybranych sąsiednich położeń.
Sporządzone wykresy dają globalny obraz zachowania się tych sum. Widzimy, że
im więcej kroków tym bardziej stabilizuje
się wartość Λ, dla położeń rozważanych
osobno, po lewej i prawej strony kierunku
celu. Nie widać również zachowań chaotycznych częściowych sum szeregu, odpowiadających odpowiednim stronom kierunku celu, a co najważniejsze wyraźnie
rysuje się ich stabilizacja i zbieżność
do wspólnej wartości obu szeregów przy n
coraz większym, a zarazem k.
Daje się też zauważyć zagęszczanie się
kroków im dalej od punktu startu, co powoduje spadek tempa zbliżania się do celu,
jeżeli ilość stawianych kroków przez marynarza w jednostce czasu jest jednakowa.
Pozostaje jeszcze kwestia „odczytu”
wartości. Wykorzystujemy w tym celu wykres, w którym wartość stanowi wspólną
asymptotę poziomą, graficznych obrazów
zależności, które przedstawia.
Biorąc z rozsądną dokładnością:
α = Λ = 0,449 = 25,74° otrzymujemy
rozwiązanie problemu marynarza z rozsądną dokładnością Λ = π/7.
Powyższy problem można też sformułować krótko i w innej postaci, a jego rozwiązanie wynika z dotychczasowych rozważań.
Kształt toru przemieszczania się marynarza na przyjętych wcześniej zasadach jest zawsze taki sam, niezależnie
od orientacji pierwszego kroku. Pytamy: czy istnieje taka prosta, która będzie przecinać tor każdego kroku marynarza i jak ją wyznaczyć?
Zauważmy, że żadna prosta łącząca
punkt wyjścia z dowolnie dalekim położeniem marynarza po wykonanym kroku nie
POLSKIE TOWARZYSTWO FIZYCZNE
SERDECZNIE ZAPRASZA NA
JUBILEUSZOWY XL ZJAZD FIZYKÓW POLSKICH
organizowany w KRAKOWIE w dniach 6–11 września 2009 r. przez Krakowski Oddział PTF
oraz Uniwersytet Jagielloński, Instytut Fizyki Jądrowej PAN, Akademię Górniczo-Hutniczą,
Politechnikę Krakowską i Uniwersytet Pedagogiczny
Dostojne grono osób objęło Zjazd patronatem honorowym. W Zjeździe weźmie udział czołówka polskich fizyków, a także kilku laureatów nagrody Nobla.
Tematyka Zjazdu obejmie najważniejsze dziedziny fizyki uprawiane w Polsce:
w Astrofizyka i historia wczesnego Wszechświata
w Energetyka
w Fizyka atomowa i molekularna
w Fizyka ciała stałego
w Fizyka jądrowa i struktura hadronów
w Fizyka matematyczna
w Fizyka medyczna
w Fizyka miękkiej materii
w Fizyka oddziaływań elementarnych
w Grawitacja kwantowa
w Nauczanie i dydaktyka fizyki
w Optyka, zimne atomy
w Teoria strun
w Zderzenia ciężkich jonów
Planujemy wykłady plenarne, sesje specjalistyczne i plakatowe oraz otwarte wykłady popularno naukowe m.in. poświęcone energetyce jądrowej.
Specjalny program szkoleniowy dla nauczycieli (sesja w niedzielę 6-go września i dwie sesje popołudniowe) obejmuje: rozstrzygnięcie dwóch konkursów
dotyczących nauczania fizyki w szkole i wręczenie nagród, sesje plakatowe, pokazy doświadczeń, multimedialne, nowoczesne formy nauczania, e-learning, wykłady popularno naukowe.
Terminy:
w do 30 marca zgłoszenia udziału
w do 30 kwietnia zgłaszanie abstraktów
w do 31 maja niższe opłaty konferencyjne
Opłaty: (obejmują: materiały konferencyjne, przyjęcie powitalne, obiady, przerwy kawowe, koncert, bankiet, wycieczkę do Kopalni Soli w Wieliczce)
w członkowie PTF:
650 zł, po 31 maja: 750 zł
w pozostali uczestnicy:
750 zł, po 31 maja: 850 zł
w nauczyciele, studenci:
350 zł, po 31 maja: 400 zł
w osoby towarzyszące:
450 zł, po 31 maja: 500 zł
Planujemy wycieczkę do Kopalni Soli w Wieliczce, gdzie będą prezentowane eksperymenty fizyczne, bankiet w Folwarku Zalesie oraz ciekawy program
kulturalny. Zakwaterowanie w hotelach i akademikach w centrum miasta.
Rejestracja i informacja: http//www. ptf. agh. edu. pl/XL-zjazd
fizyka wczoraj, dziś i jutro
kroków „zmierzają” do jednego wspólnego
kierunku (do nałożenia się na siebie), co
uzasadnia istnienie takiej prostej.
A jest to prosta przechodząca przez
punkt startu pod kątem α = Λ = 25,74°
do kierunku pierwszego kroku w stronę,
której wybór nasuwa się sam w oczywisty
sposób.
Najważniejsze wnioski, płynące z naszych rozważań, pozwalają określić kierunek celu już po pierwszym kroku,
a przede wszystkim zaprogramować
pierwszy krok dla dowolnego kierunku
celu z każdego punktu płaszczyzny.
L
c
ITERATURA
[1] Feynman, Wykłady z fizyki, t. I, cz. 2, PWN,
Warszawa 1974.
Rys. 3.
HIERONIM LALEK
może być tą prostą, gdyż każdy następny
krok już jej nie przecina (rys. 2).
Jeżeli kąt odchylenia maleje i zmierza
do zera w nieskończoności, to dwie proste,
łączące punkt wyjścia z dwoma sąsiednimi
i bardzo dalekimi położeniami, leżą coraz
bliżej siebie i wraz z liczbą wykonanych
LO Rymanów, 38-480 Rymanów, Szkolna 5a/16
e-mail: [email protected]
BARTOSZ LALEK
Zespół Szkół Kształcenia Ustawicznego
w Krośnie
Szanowni Czytelnicy
Uprzejmie przypominamy, że w czerwcu upływa termin
zamówienia prenumeraty „Fizyki w Szkole”
na II półrocze roku 2009.
Szczegółowe warunki prenumeraty na s. 66.
Redakcja
18
fizyka w szkole