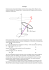1. SKŁADOWA RADIALNA I TRANSWERSALNA WEKTORA

MECHANIKA TEORETYCZNA
1. SKŁADOWA RADIALNA I TRANSWERSALNA WEKTORA
PĘDKOŚĆI I PRZYŚPIESZENIA
Pod pojęciem PUNKTU MATERIALNEGO rozumiemy twór fizyczny o znikomo
małych rozmiarach, obdarzony masą, którego położenie w każdej chwili ruchu
możemy rozpatrywać jak położenie punktu geometrycznego.
Przy opisywaniu położenia takiego punktu w zadanym układzie odniesienia

(układzie współrzędnych) posłużymy się WEKTOREM WODZĄCYM r o początku w
początku układu współrzędnych a końcu P w danym punkcie.
y
r
P
j
k
x
i
z
W układzie trójwymiarowym wektor wodzący można rozpisać na składowe:

r  iˆ x  ˆj y  kˆz
Gdzie iˆ, ˆj , kˆ są wersorami jednostkowymi odpowiednich osi.
Aby móc mówić o RUCHU należy znaleźć zmianę tego wektora w czasie:

r (t )  iˆx(t )  ˆjy(t )  kˆz(t )
Wyrażenie na ruch można zapisać w wygodniejszej postaci parametrycznej. Postać
ta, bowiem w prosty sposób opisuje TOR RUCHU:
 x(t )  x

 y (t )  y
 z (t )  z

Zgodnie z założeniem funkcje te muszą być ciągłe i dwukrotnie różniczkowalne.
PRĘDKOŚĆ punktu materialnego jest wektorem danym przez pierwszą
pochodną promienia wodzącego względem czasu.
 dr d
dx(t ) ˆ dy (t ) ˆ dz (t ) ˆ
diˆ
dˆj
dkˆ
V 
iˆx(t )  ˆjy (t )  kˆz (t ) 
i
j
k  x(t )  y (t )  z (t )

dt dt
dt
dt
dt
dt
dt
dt
Wiedząc, że iˆ, ˆj , kˆ są stałe ich pochodne są równe 0.
 dx(t )
dy (t ) ˆ dz (t ) ˆ
V 
iˆ 
j
k  0  0  0  iˆx  ˆjy  kˆz
dt
dt
dt


V  iˆ x  ˆj y  kˆz  r


Opracowanie: Katarzyna Grzelczak
1
MECHANIKA TEORETYCZNA
PRZYŚPIESZENIE punktu materialnego wyraża wektor dany pierwszą pochodną
prędkości względem czasu, zatem:

 dV d ˆ

a
 (i x  ˆjy  kˆz)  r
dt
dt
W przypadku ruchu płaskiego (dwuwymiarowego) wygodniej jest posłużyć się

UKŁADEM BIEGUNOWEGO współrzędnych r ,  .
y
r
φ
x

Układ ten opiera się na wektorze wodzącym r oraz kącie  , jaki tworzy wektor
wodzący z x-ową osią współrzędnych. W tym przypadku często praktykuje się
rozkład wektorów prędkości i przyśpieszenia na SKŁADOWĄ RADIALNĄ, która

wskazuje nam kierunek wektora wodzącego r (Vr , a r ) oraz na SKŁADOWĄ
TRAWNWERSALNĄ styczną do okręgu o promieniu r , której zwrot pokaże nam
kierunek przyrostu kąta  (V , a ) .
Obierając więc układ współrzędnych płaski-dwuwymiarowy postać wektora
wodzącego sprowadza się do:

r  iˆx  ˆjy
Wprowadźmy teraz zamiast wektora wodzącego liczbę zespoloną z , która
również określa położenie punktu materialnego:
z  x  iy
Gdzie i oczywiście jest liczbą urojoną, x - współrzędną rzeczywistą, y natomiast
współrzędną zespoloną.
Liczbę zespoloną można zapisać również w postaci Eulera:
z  e i  r cos   i sin  
Wektor prędkości w układzie biegunowym:
 
V  r  iˆx  ˆjy
Dla liczby zespolonej:
d
z  x  iy  r  ei  rei  rei  i  ei (r  ir)
dt
Zatem:
 ˆ
 r  i x  ˆjy

i
 z  e (r  ir )


Opracowanie: Katarzyna Grzelczak
2
MECHANIKA TEORETYCZNA
Wektor przyśpieszenia w układzie biegunowym:
 
a  r  iˆx  ˆjy
Dla liczby zespolonej:
d i
d
z 
e (r  ir )  e i  i r  ir   e i r  ir   e i i  r  r 2   e i r  i r  r 
dt
dt
i
2
i
i
 e i  r  r   e r  ir  ir  e r  r 2  i 2r  r
Zatem:
 ˆ

r  i x  ˆjy

i
2
z  e r  r  i 2r  r



Obierzmy teraz dowolny wektor k [ x, y ] w płaszczyźnie xy:
k’
Ф
y
φ
k
z
φ
x

k  iˆk x  ˆjk y

k  k x  ik y  k  e i

Aby otrzymać liczbę zespoloną odpowiadającą wektorowi k , której część
rzeczywista i zespolona były jego składowymi w układzie biegunowym musimy
dokonać obrotu układu o początku w punkcie z i osiach xy o kąt  . Przy tym obrocie

kąt  określający kierunek wektora k w płaszczyźnie xy przechodzi na kąt     .

k  k  e i

k   k r  ik

k   k  e     k  e i  e  i
Zatem:

 k  k  e i

i
i
k   k  e  e
A więc by przedstawić w układzie obróconym o kąt  wektor dany przez liczbę
zespoloną należy ją pomnożyć przez e  i . Zatem korzystając z tej informacji:
k r  ik  k  e i   
k r  ik  k x  ik y   e i
Opracowanie: Katarzyna Grzelczak
3
MECHANIKA TEORETYCZNA
Dla wektorów prędkości i przyśpieszenia będzie wyglądało to następująco:
Vr  iV  r  ir
Vr  iV  z  e i




2
i
ar  ia  z  e
ar  ia  r  r  i2r  r
Zatem:
 Vr  r
 a r  r  r 2
oraz




a  2r  r
V  r
LITERATURA
1. Notatki z wykładu dr hab., nauk fizycznych – prof. ndzw. Grzegorza Bąka
2. „Mechanika Teoretyczna” W. Rubinowicz, W. Królikowski
Opracowanie: Katarzyna Grzelczak
4