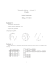Matematyka Dyskretna 8/2008 1. Cząsteczki węglowodoru składają

Cz. Bagiński – Materiały dydaktyczne
Matematyka Dyskretna 8/2008
1. Cząsteczki węglowodoru składają się z atomów węgla (o wartościowości 4) i atomów wodoru (o
wartościowości 1) i mogą być przedstawione jako grafy spójne. Dla przykładu zarówno cząsteczka
butanu, jak i 2-metylopropanu (izobutanu) zawierają cztery atomy węgla i dziesięć atomów wodoru
połączonych tak, jak pokazują to rysunki:
r
r
r
r
r
r
s
s
s
s
r
r
r
r
r
r
s
r
s
r
r
@
r @s
@s
r @
r @r
@r
Te dwie nieizomorficzne struktury o wzorze chemicznym C4 H10 są przykładami izomerów. Pokazać,
że:
(a) Każda cząsteczka węglowodoru o wzorze postaci Cn H2n+2 (zwana parafiną lub alkanem) ma
strukturę drzewa, natomiast cząsteczki o wzorze postaci Cn H2n (alkeny) nie mają struktury drzewa.
(b) Udowodnić, że powyższe dwa przykłady są jedynymi izomerami postaci C4 H10 i wyznaczyć
największą możliwą liczbę izomerów postaci C5 H12 .
2. Ile jest różnych maksymalnych drzew zawartych w grafie dwudzielnym K2,n ?
3. Wachlarzem rzędu n nazywamy graf, którego zbiorem wierzchołków jest {0, 1, 2, . . . , n} i który
ma 2n − 1 krawędzi zdefiniowanych następująco: wierzchołek 0 jest połączony krawędzią z każdym z
pozostałych wierzchołków, ponadto dla każdego k, 1 6 k < n, wierzchołek k jest połączony krawędzię
z wierzchołkiem k + 1. Wyznacz ile jest różnych maksymalnych drzew zawartych w tym grafie.
4. Ile jest różnych oznakowanych drzew o zbiorze wierzchołków {1, 2, . . . , n}, które mają
(a) wierzchołek stopnia n − 1?
(b) wierzchołek stopnia n − 2?
(c) stopień wierzchołka 1 jest równy 1?
5. Wyznaczyć liczby wszystkich drzew maksymalnych zawartych w grafach wielościanów foremnych.
6. Ile jest wszystkich drzew bez wierzchołków stopnia 2, spinających graf pełny o siedmiu ponumerowanych wierzchołkach? Ile jest takich drzew parami nieizomorficznych? Ile jest wszystkich oznakowanych
drzew bez wierzchołków stopnia 5 i 4 spinających graf pełny o 7 ponumerowanych wierzchołkach? Ile
wśród nich można znaleźć drzew parami nieizomorficznych?
7. Zbadać, czy grafy opisane w zadaniach 8 i 9 z zestawu 7/2008 są eulerowskie oraz hamiltonowskie.
8. Udowodnić, że następujący graf (zwany grafem Herschela) nie jest Hamiltonowski. Jest to minimalny graf 3-spójny o 11 wierzchołkach nie będący grafem Hamiltona.
t
H
A HH
t AAtH HH
@
HHt HHt
t t
H
H @t
HH H
@
Ht @t
H
HHAA H
A
t
Cz. Bagiński – Materiały dydaktyczne
9. Niech G = (V, E) będzie grafem, którego zbiorem wierzchołków jest
V = {(a1 , a2 , a3 , a4 )| 1 6 ai 6 4, ai ∈ N, ai 6= aj , dla i 6= j}.
Dwa ciągi ze zbioru V łączy krawędź należąca do E wtedy i tylko wtedy, gdy jeden z tych ciągów
można otrzymać z drugiego przez zamianę miejscami dwóch sąsiednich wyrazów. Udowodnić, że graf
ten jest hamiltonowski i jest izomorficzny z grafem
u
u
@
@`
u
u `
``u
u
D
B
D
BP
u
D u
P
D
Pu
u @
@u u
u u
u
@
P
u
PPu
@
u
D
D
B
D
Bu
`
u
`
``Du
u
@
@u
u
10. Czy poniższe grafy są hamiltonowskie?
u
u
u
u
u
u
u
u
u
u
u
u
u u
u
u
tP
P
B PPP
PP
B
Pt
t
B @
AA
@
B
At
@t
B
At
@t
B
A
@
Bt
@t At
H
HHt
HH
t
Ht
t
t
t
t
t
t
u
u
u
u
u
u
u
u
u
u t
t
t
t
t
t
t
t
t
t
t t
t
t
t
t
t
t
t
t
t
t
t
t
t
HHt
HH
t
t
t
H
Ht
A
@
B
t
t
A
@
B
At
@ t
B
A
@
B
AAtP
@
@t B
PP
PP B
PP
PB t
Przygotował: Cz. Bagiński